题目内容
8．给出以下四组线段①a=7，b=24，c=25．②a=32，b=42，c=52．③a=$\sqrt{41}$，b=4，c=5．④a=13，b=14，c=15．由线段a，b，c组成直角三角形的有（ ）组．| A． | 4 | B． | 3 | C． | 2 | D． | 1 |
分析 根据勾股定理的逆定理知，当三角形的三边关系为：a2+b2=c2时，它是直角三角形，由此可解出本题．
解答 解：①中有72+242=252；
②（32）2+（42）2≠（52）2；
③中有42+52=（$\sqrt{41}$）2；
④132+142≠152；
所以可以构成2组直角三角形．
故选C．
点评 本题考查了勾股定理的逆定理，由勾股定理的逆定理，只要验证两小边的平方和等于最长边的平方即可．
练习册系列答案
相关题目
19．下列式子中，属于最简二次根式的是（ ）
| A． | $\sqrt{13}$ | B． | $\sqrt{20}$ | C． | $\sqrt{8}$ | D． | $\frac{1}{\sqrt{2}}$ |
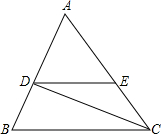如图，CD是∠ACB的平分线，∠EDC=25°，∠DCE=25°，∠B=70°．
如图，每个小正方形的边长为1．