题目内容
关于x的一元二次方程kx2-3x-1=0有两个不相等的实数根.
(1)求k的取值范围;
(2)请选择一个k的负整数值,并求出方程的根.
(1)求k的取值范围;
(2)请选择一个k的负整数值,并求出方程的根.
考点:根的判别式
专题:
分析:(1)根据一元二次方程的定义及根的判别式列出关于k的不等式,求出k的取值范围即可;
(2)选择一个k的负整数值,求出方程的根即可.
(2)选择一个k的负整数值,求出方程的根即可.
解答:解:(1)∵关于x的一元二次方程kx2-3x-1=0有两个不相等的实数根,
∴
,解得k>-
且k≠0;
(2)当k=-2时,原方程可化为-2x2-3x-1=0,解得x1=-1,x2=
.
∴
|
| 9 |
| 4 |
(2)当k=-2时,原方程可化为-2x2-3x-1=0,解得x1=-1,x2=
| 1 |
| 2 |
点评:本题考查的是根的判别式,熟知一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac的关系是解答此题的关键.

练习册系列答案
相关题目
 如图,在△ABC中,点D,F分别在边AC,BC上,且满足
如图,在△ABC中,点D,F分别在边AC,BC上,且满足| AB |
| AD |
| AC |
| AB |
A、1:
| ||
| B、1:2 | ||
| C、1:3 | ||
| D、1:4 |
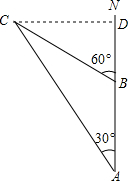 如图所示,一艘货船以30 km/h的速度向正北航行,在A出看见灯塔C在船的北偏西30°,20s后货船航行至B处,看见灯塔C在船的北偏西60°,若货船向北继续航行,当灯塔C在船的正西方向时,灯塔与货船相距多少米(精确到0.1m)?
如图所示,一艘货船以30 km/h的速度向正北航行,在A出看见灯塔C在船的北偏西30°,20s后货船航行至B处,看见灯塔C在船的北偏西60°,若货船向北继续航行,当灯塔C在船的正西方向时,灯塔与货船相距多少米(精确到0.1m)? 已知反比例函数图象y=
已知反比例函数图象y=