题目内容
小王假期想去勤工俭学,每天从某报社以每份0.5元买进200份报纸,再以每份1元卖给读者,报纸没卖完的话,当天可退回报社,但报社只按每份0.2元退给小王.
(1)若设小王每天平均卖出x份报纸,用含x的代数式表示:
①卖出x份报纸可获利 元;
②没卖出的报纸 份,亏损 元.
(2)请问小王平均每天至少要卖出多少份报纸才能使每月(按30天计算)总收入不低于2000元?
(1)若设小王每天平均卖出x份报纸,用含x的代数式表示:
①卖出x份报纸可获利
②没卖出的报纸
(2)请问小王平均每天至少要卖出多少份报纸才能使每月(按30天计算)总收入不低于2000元?
考点:一元一次不等式的应用
专题:
分析:(1)①根据题意可知,卖一份报纸赚0.5元,求出卖出x份报纸获利为0.5x元;
②根据题意求出没卖出的报纸以及亏损;
(2)设小王每天平均卖出x份报纸,根据月总收入不低于2000元,列不等式求解.
②根据题意求出没卖出的报纸以及亏损;
(2)设小王每天平均卖出x份报纸,根据月总收入不低于2000元,列不等式求解.
解答:解:(1)①卖出x份报纸获利为0.5x元;
②由题意得,没卖出的报纸为200-x份,
亏损为:(0.5-0.2)(200-x)=0.3(200-x),
故答案为:0.5x;200-x;0.3(200-x);
(2)设小王每天平均卖出x份报纸,
由题意得,[0.5x-0.3(200-x)]×30≥2000,
解得:x≥158
,
答:小王平均每天至少要卖出159份报纸才能使每月(按30天计算)总收入不低于2000元.
②由题意得,没卖出的报纸为200-x份,
亏损为:(0.5-0.2)(200-x)=0.3(200-x),
故答案为:0.5x;200-x;0.3(200-x);
(2)设小王每天平均卖出x份报纸,
由题意得,[0.5x-0.3(200-x)]×30≥2000,
解得:x≥158
| 1 |
| 3 |
答:小王平均每天至少要卖出159份报纸才能使每月(按30天计算)总收入不低于2000元.
点评:本题考查了一元一次不等式的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系和不等关系,列不等式求解.

练习册系列答案
相关题目
下列各数是无理数的是( )
A、
| |||
B、
| |||
C、
| |||
| D、-π |
若x2+xy=-3,xy+y2=5,则x2+2xy+y2的值为( )
| A、2 | B、-2 | C、8 | D、-8 |
实数-
,0,
,-2π,
,0.1010001000001…(两个1之间依次多两个0)中,无理数的个数有( )
| 8 |
| 7 |
| 6 |
| 3 | -125 |
| A、3个 | B、4个 | C、5个 | D、6个 |
如果(a+3)2+|b-2|=0,那么代数式(a+b)2015的值是( )
| A、-2015 | B、2015 |
| C、1 | D、-1 |
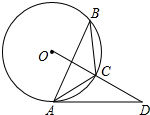 已知:如图,△ABC内接于⊙O,点D在OC的延长线上,∠B=∠CAD=30°.
已知:如图,△ABC内接于⊙O,点D在OC的延长线上,∠B=∠CAD=30°.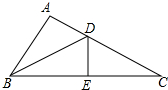 已知在△ABC中,∠A=90°,D,E分别是边BC,AC上的点,且DE⊥BC于D,△ADB≌△EDB≌EDC,则∠C的度数为多少?.DE与DC之间有怎样的数量关系?说明理由.
已知在△ABC中,∠A=90°,D,E分别是边BC,AC上的点,且DE⊥BC于D,△ADB≌△EDB≌EDC,则∠C的度数为多少?.DE与DC之间有怎样的数量关系?说明理由.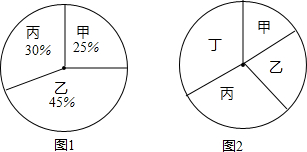 分别求出每个扇形的圆心角的度数.
分别求出每个扇形的圆心角的度数.