题目内容
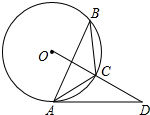 已知:如图,△ABC内接于⊙O,点D在OC的延长线上,∠B=∠CAD=30°.
已知:如图,△ABC内接于⊙O,点D在OC的延长线上,∠B=∠CAD=30°.(1)求证:AD是⊙O的切线;
(2)若OD⊥AB,BC=4,求AD的长.
考点:切线的判定
专题:
分析:(1)连接OA,由已知∠B=∠CAD=30°,所以得∠AOC=60°,继而可得∠OAC=60°,又∠CAD=30°,所以∠OAD=90°,问题得证;
(2)由于OD⊥AB,OC是半径,利用垂径定理可知OC是AB的垂直平分线,那么CA=CB,而∠B=30°,则∠D=30°,通过解直角三角形求得AD的长度即可.
(2)由于OD⊥AB,OC是半径,利用垂径定理可知OC是AB的垂直平分线,那么CA=CB,而∠B=30°,则∠D=30°,通过解直角三角形求得AD的长度即可.
解答: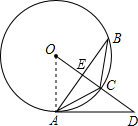 (1)证明:连接OA,
(1)证明:连接OA,
∵∠B=30°,
∴∠AOC=60°,
可得∠OAC=60°,
又∵∠CAD=30°,
∴∠OAD=90°,
∴AD是⊙O的切线;
(2)解:∵OD⊥AB,
∴弧BC=弧AC,
∴BC=AC=4,
∵△OAC是等边三角形,
∴OA=AC=4,
在Rt△OAD中,∠D=30°,OA=4,
∴AD=4
.
 (1)证明:连接OA,
(1)证明:连接OA,∵∠B=30°,
∴∠AOC=60°,
可得∠OAC=60°,
又∵∠CAD=30°,
∴∠OAD=90°,
∴AD是⊙O的切线;
(2)解:∵OD⊥AB,
∴弧BC=弧AC,
∴BC=AC=4,
∵△OAC是等边三角形,
∴OA=AC=4,
在Rt△OAD中,∠D=30°,OA=4,
∴AD=4
| 3 |
点评:此题考查了切线的判定与性质,圆周角定理,等边三角形的判定与性质,以及锐角三角函数定义,熟练掌握切线的判定与性质是解本题的关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
零是( )
| A、正数 | B、奇数 | C、负数 | D、偶数 |
下列事件中,属于必然事件的是( )
| A、明天会下雨 |
| B、三角形两边之和大于第三边 |
| C、两个数的和大于每一个加数 |
| D、在一个没有红球的盒子里,摸到红球 |
小明近期几次数学测试成绩如下:第一次85分,第二次比第一次高9分,第三次比第二次低12分,第四次又比第三次高10分.那么小明第四次测验的成绩是( )
| A、72分 | B、82分 |
| C、92分 | D、94分 |
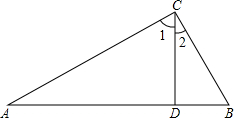 如图,∠ACB=90°,CD⊥AB,垂足为点D,下列结论错误的是( )
如图,∠ACB=90°,CD⊥AB,垂足为点D,下列结论错误的是( )| A、∠A=∠2 |
| B、∠1和∠B都是∠A的余角 |
| C、∠1=∠2 |
| D、图中有3个直角三角形 |
下列计算正确的是( )
A、
| |||
B、
| |||
C、
| |||
D、
|
一个数的平方是25,则这个数是( )
| A、5 | ||||
| B、-5 | ||||
| C、5或-5 | ||||
D、
|
下列变形中正确的是( )
| A、x2-(-x+y)=x2+x-y |
| B、3a-(b+c-d)=3a-b+c-d |
| C、4+2(a-b)=4+2a-b |
| D、a+(b-c)=ab-c |