题目内容
16.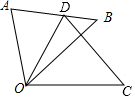 如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠B的度数是( )
如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠B的度数是( )| A. | 40° | B. | 35° | C. | 30° | D. | 15° |
分析 根据旋转的性质可得∠AOD=∠BOC=30°,AO=DO,再求出∠BOD,∠ADO,然后利用三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
解答 解:∵△COD是△AOB绕点O顺时针旋转40°后得到的图形,
∴∠AOD=∠BOC=30°,AO=DO,
∵∠AOC=100°,
∴∠BOD=100°-30°×2=40°,
∠ADO=∠A=$\frac{1}{2}$(180°-∠AOD)=$\frac{1}{2}$(180°-30°)=75°,
由三角形的外角性质得,∠B=∠ADO-∠BOD=75°-40°=35°.
故选B.
点评 本题考查了旋转的性质,等腰三角形的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质并准确识图是解题的关键.

练习册系列答案
相关题目
6.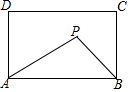 如图,在矩形ABCD中,AB=5,AD=3,动点P满足S△PAB=$\frac{1}{3}$S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为( )
如图,在矩形ABCD中,AB=5,AD=3,动点P满足S△PAB=$\frac{1}{3}$S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为( )
 如图,在矩形ABCD中,AB=5,AD=3,动点P满足S△PAB=$\frac{1}{3}$S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为( )
如图,在矩形ABCD中,AB=5,AD=3,动点P满足S△PAB=$\frac{1}{3}$S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为( )| A. | $\sqrt{29}$ | B. | $\sqrt{34}$ | C. | 5$\sqrt{2}$ | D. | $\sqrt{41}$ |

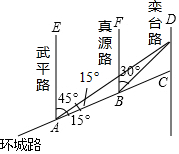 如图,AC是某市环城路的一段,AE、BF、CD都是南北方向的街道,其与环城路AC的交叉路口分别是A、B、C经测量东方家具城D位于点A的北偏东45°方向,点B的北偏东30°方向上,AB=2km,∠DAC=15°,求C、D之间的距离(结果保留根号).
如图,AC是某市环城路的一段,AE、BF、CD都是南北方向的街道,其与环城路AC的交叉路口分别是A、B、C经测量东方家具城D位于点A的北偏东45°方向,点B的北偏东30°方向上,AB=2km,∠DAC=15°,求C、D之间的距离(结果保留根号). 某乡镇准备在相距3千米的A、B两个工厂间修建一条笔直的公路,在工厂A北偏东60°方向,工厂北偏西45°方向有一点P,以P点为圆心,1.2千米为半径的区域是一个村庄,问修筑公路时,这个村庄是否有居民需要搬迁?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
某乡镇准备在相距3千米的A、B两个工厂间修建一条笔直的公路,在工厂A北偏东60°方向,工厂北偏西45°方向有一点P,以P点为圆心,1.2千米为半径的区域是一个村庄,问修筑公路时,这个村庄是否有居民需要搬迁?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)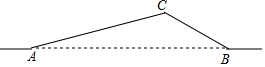 如图,从A地到B地的公路需经过C地,图中AC=6千米,∠CAB=15°,∠CBA=30°.因城市规划的需要,将在A、B两地之间修建一条笔直的公路.
如图,从A地到B地的公路需经过C地,图中AC=6千米,∠CAB=15°,∠CBA=30°.因城市规划的需要,将在A、B两地之间修建一条笔直的公路. 如图,在Rt△ACB中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.
如图,在Rt△ACB中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.