题目内容
6.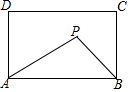 如图,在矩形ABCD中,AB=5,AD=3,动点P满足S△PAB=$\frac{1}{3}$S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为( )
如图,在矩形ABCD中,AB=5,AD=3,动点P满足S△PAB=$\frac{1}{3}$S矩形ABCD,则点P到A、B两点距离之和PA+PB的最小值为( )| A. | $\sqrt{29}$ | B. | $\sqrt{34}$ | C. | 5$\sqrt{2}$ | D. | $\sqrt{41}$ |
分析 首先由S△PAB=$\frac{1}{3}$S矩形ABCD,得出动点P在与AB平行且与AB的距离是2的直线l上,作A关于直线l的对称点E,连接AE,连接BE,则BE的长就是所求的最短距离.然后在直角三角形ABE中,由勾股定理求得BE的值,即PA+PB的最小值.
解答  解:设△ABP中AB边上的高是h.
解:设△ABP中AB边上的高是h.
∵S△PAB=$\frac{1}{3}$S矩形ABCD,
∴$\frac{1}{2}$AB•h=$\frac{1}{3}$AB•AD,
∴h=$\frac{2}{3}$AD=2,
∴动点P在与AB平行且与AB的距离是2的直线l上,如图,作A关于直线l的对称点E,连接AE,连接BE,则BE的长就是所求的最短距离.
在Rt△ABE中,∵AB=5,AE=2+2=4,
∴BE=$\sqrt{A{B}^{2}+A{E}^{2}}$=$\sqrt{{5}^{2}+{4}^{2}}$=$\sqrt{41}$,
即PA+PB的最小值为$\sqrt{41}$.
故选D.
点评 本题考查了轴对称-最短路线问题,三角形的面积,矩形的性质,勾股定理,两点之间线段最短的性质.得出动点P所在的位置是解题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
16.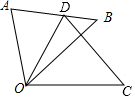 如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠B的度数是( )
如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠B的度数是( )
 如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠B的度数是( )
如图,△ODC是由△OAB绕点O顺时针旋转30°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为100°,则∠B的度数是( )| A. | 40° | B. | 35° | C. | 30° | D. | 15° |
14.某公司有15名员工,他们所在部门及相应每人所创年利润如下表所示:
这15名员工每人所创年利润的众数、中位数分别是( )
| 部门 | 人数 | 每人所创年利润(单位:万元) |
| A | 1 | 10 |
| B | 3 | 8 |
| C | 7 | 5 |
| D | 4 | 3 |
| A. | 10,5 | B. | 7,8 | C. | 5,6.5 | D. | 5,5 |
1. 如图,一个放置在水平实验台上的锥形瓶,它的俯视图为( )
如图,一个放置在水平实验台上的锥形瓶,它的俯视图为( )
 如图,一个放置在水平实验台上的锥形瓶,它的俯视图为( )
如图,一个放置在水平实验台上的锥形瓶,它的俯视图为( )| A. |  | B. |  | C. |  | D. |  |




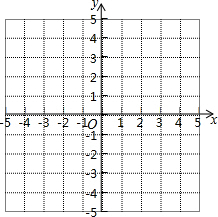 已知:一次函数y=2x+4
已知:一次函数y=2x+4