题目内容
1. 已知二次函数y=-x2+bx+c的部分图象如图所示,则不等式-x2+bx+c>0的解集是-1<x<3.
已知二次函数y=-x2+bx+c的部分图象如图所示,则不等式-x2+bx+c>0的解集是-1<x<3.
分析 由对称轴x=1,抛物线与x轴的交点(3,0),根据二次函数的对称性求得另一个与x轴交点的坐标根据图象与x轴交点的坐标即可得到不等式-x2+bx+c>0的解集.
解答 解:∵对称轴x=1,抛物线与x轴的交点(3,0),
∴另一个与x轴交点的坐标(-1,0),
∴二次函数y=-x2+2x+c的图象与x轴交点坐标为(-1,0)、(3,0),
而-x2+2x+c>0,
即y>0,
∴-1<x<3.
故答案为:-1<x<3.
点评 此题主要考查了二次函数与一元二次不等式之间的联系,利用图象以及二次函数的性质解决问题.

练习册系列答案
相关题目
9.张明的父母打算购买一种形状和大小都相同的正多边形瓷砖来铺地板,为了保证铺地板时既没缝隙,又不重叠,则所购瓷砖形状不能是( )
| A. | 正三角形 | B. | 正方形 | C. | 正六边形 | D. | 正八边形 |
8.A、B两点关于直线l对称,点P是直线l上一点,若PA=4cm,则PB等于( )
| A. | 2cm | B. | 4cm | C. | 6cm | D. | 不能确定 |
 如图,已知△ABC.
如图,已知△ABC.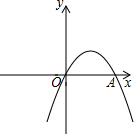 如图,抛物线y=-x2+bx+c经过坐标原点,并与x轴相交于点A(2,0).
如图,抛物线y=-x2+bx+c经过坐标原点,并与x轴相交于点A(2,0).