题目内容
1.如图1所示,已知y=$\frac{6}{x}$(x>0)图象上一点P,PA⊥x轴于点A(a,0),点B坐标为(0,b)(b>0),动点M是y轴正半轴上B点上方的点,动点N在射线AP上,过点B作AB的垂线,交射线AP于点D,交直线MN于点Q连接AQ,取AQ的中点为C.(1)如图2,连接BP,求△PAB的面积;
(2)当点Q在线段BD上时,若四边形BQNC是菱形,面积为4$\sqrt{3}$,求此时P点的坐标;
(3)当点Q在射线BD上时,且a=6,b=2,若以点B,C,N,Q为顶点的四边形是平行四边形,求这个平行四边形的周长.
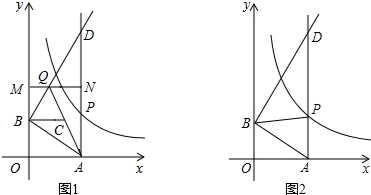
分析 (1)根据同底等高的两个三角形的面积相等即可求出△PAB的面积;
(2)连接BN,CN,首先求出∠BQC=60°,∠BAQ=30°,然后证明△ABQ≌△ANQ,进而求出∠BAO=30°,由S四边形BQNC=4$\sqrt{3}$,求出OA=3,于是P点坐标求出;
(3)分两类进行讨论,当点Q在线段BD上,根据题干条件求出AQ的长,进而求出四边形的周长,当点Q在线段BD的延长线上,依然根据题干条件求出AQ的长,再进一步求出四边形的周长.
解答  解:(1)如图1,连接OP.
解:(1)如图1,连接OP.
S△PAB=S△PAO=$\frac{1}{2}$xy=$\frac{1}{2}$×6=3;
(2)如图2,连接BN,CN,
∵四边形BQNC是菱形,
∴BQ=BC=NQ,∠BQC=∠NQC,
∵AB⊥BQ,C是AQ的中点,
∴BC=CQ=$\frac{1}{2}$AQ,
∴∠BQC=60°,∠BAQ=30°,
在△ABQ和△ANQ中,
$\left\{\begin{array}{l}BQ=NQ\\∠BQA=∠NQA\\ QA=QA\end{array}\right.$,
∴△ABQ≌△ANQ(SAS),
∴∠BAQ=∠NAQ=30°,
∴∠BAO=30°,
∵S菱形BQNC=4$\sqrt{3}$=$\frac{1}{2}$×CQ×BN,
令CQ=2t=BQ,则BN=2×(2t×$\frac{\sqrt{3}}{2}$)=2$\sqrt{3}$t,
∴t=1
∴BQ=2,
∵在Rt△AQB中,∠BAQ=30°,
∴AB=$\sqrt{3}$BQ=2$\sqrt{3}$,
∵∠BAO=30°
∴OA=$\frac{\sqrt{3}}{2}$AB=3,
又∵P点在反比例函数y=$\frac{6}{x}$的图象上,
∴P点坐标为(3,2);
(3)∵a=6,b=2,
∴OB=2,OA=6,
∴AB=$\sqrt{36+4}$=2$\sqrt{10}$,
易得△AOB∽△DBA,
∴$\frac{OB}{OA}$=$\frac{AB}{BD}$,
∴BD=6$\sqrt{10}$.
①如图3,当点Q在线段BD上,
∵AB⊥BD,C为AQ的中点,
∴BC=$\frac{1}{2}$AQ,
∵四边形BQNC是平行四边形,
∴QN=BC,CN=BQ,CN∥BD,
∴$\frac{CN}{QD}$=$\frac{AC}{AQ}$=$\frac{1}{2}$,
∴BQ=CN=$\frac{1}{3}$BD=2$\sqrt{10}$,
∴AQ=$\sqrt{{AB}^{2}+{BQ}^{2}}$=4$\sqrt{5}$,
∴C四边形BQNC=4$\sqrt{10}$+4$\sqrt{5}$;
②如图4,当点Q在射线BD的延长线上,
∵AB⊥BD,C为AQ的中点,
∴BC=CQ=$\frac{1}{2}$AQ,
∴平行四边形BNQC是菱形,BN=CQ,BN∥CQ,
∴△BND∽△QAD
∴$\frac{BD}{QD}$=$\frac{BN}{AQ}$=$\frac{1}{2}$,
∴BQ=3BD=18$\sqrt{10}$,
∴AQ=$\sqrt{{BQ}^{2}+{AB}^{2}}$=$\sqrt{{(18\sqrt{10})}^{2}+{(2\sqrt{10})}^{2}}$=4$\sqrt{205}$,
∴C四边形BNQC=2AQ=4$\sqrt{205}$.
综上所述,这个平行四边形的周长为4$\sqrt{10}$+4$\sqrt{5}$或4$\sqrt{205}$.
点评 本题主要考查反比例函数综合题的知识,此题涉及的知识有全等三角形的判定与性质、相似三角形的性质以及菱形等知识,综合性较强,有一定的难度.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 0-$\frac{1}{2}$=$\frac{1}{2}$ | B. | (-1)+(-$\frac{1}{2}$)=$\frac{3}{2}$ | C. | 2×(-$\frac{1}{2}$)=1 | D. | 2÷(-$\frac{1}{2}$)=-4 |
| A. | 2cm | B. | 4cm | C. | 6cm | D. | 不能确定 |
 如图,已知△ABC.
如图,已知△ABC. =__________。
=__________。