题目内容
9.求代数式$(\frac{1}{x+y}-\frac{1}{x-y})÷\frac{{x{y^2}}}{{{x^2}-{y^2}}}$的值,(其中x=3,y=-2).分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x与y的值代入计算即可求出值.
解答 解:原式=($\frac{x-y}{(x+y)(x-y)}$-$\frac{x+y}{(x+y)(x-y)}$)•$\frac{(x+y)(x-y)}{x{y}^{2}}$=$\frac{-2y}{(x+y)(x-y)}$•$\frac{(x+y)(x-y)}{x{y}^{2}}$=$\frac{-2}{xy}$,
当x=3,y=-2时,原式=$\frac{1}{3}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
20.下列计算中,正确的是( )
| A. | 2a2+3a2=5a4 | B. | (a-b)2=a2-b2 | C. | (a3)3=a6 | D. | (-2a2)3=-8a6 |
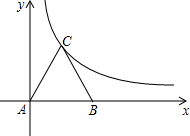 如图,等边△ABC放置在平面直角坐标系中,已知A(0,0)、B(2,0),反比例函数的图象经过点C.
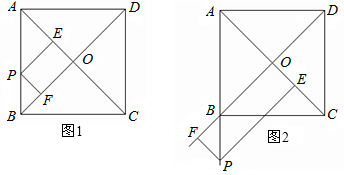
如图,等边△ABC放置在平面直角坐标系中,已知A(0,0)、B(2,0),反比例函数的图象经过点C. 如图,边长为2的正方形ABCD中,点E、F分别在BC,CD上,△AEF是等边三角形,连接AC交EF 于G,下列结论:①∠DAF=15°;②AC垂直平分EF;③BE+DF=EF;④S△CEF=2S△ABE,其中正确结论是( )
如图,边长为2的正方形ABCD中,点E、F分别在BC,CD上,△AEF是等边三角形,连接AC交EF 于G,下列结论:①∠DAF=15°;②AC垂直平分EF;③BE+DF=EF;④S△CEF=2S△ABE,其中正确结论是( )