题目内容
3. 如图,边长为2的正方形ABCD中,点E、F分别在BC,CD上,△AEF是等边三角形,连接AC交EF 于G,下列结论:①∠DAF=15°;②AC垂直平分EF;③BE+DF=EF;④S△CEF=2S△ABE,其中正确结论是( )
如图,边长为2的正方形ABCD中,点E、F分别在BC,CD上,△AEF是等边三角形,连接AC交EF 于G,下列结论:①∠DAF=15°;②AC垂直平分EF;③BE+DF=EF;④S△CEF=2S△ABE,其中正确结论是( )| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
分析 根据正方形的性质和全等三角形的判定和性质对各项逐一判断即可.
解答 解:∵四边形ABCD是正方形,
∴AB=BC=CD=DA,∠B=∠D=90°,
∵△AEF是等边三角形,
∴AE=AF,
∴△ABE≌△ADF,
∴BE=DF,
∴EC=FC,
又∵AC=AC,
∴△AEC≌△AFC,
∴∠EAC=∠FAC=30°,
∴AC垂直平分EF,故②成立;
∴∠DAF=∠CAD-∠FAC=45°-30°=15°,故①成立;
设BE=DF=x,则EC=FC=2-x,
∴$EF=\sqrt{E{C^2}+F{C^2}}=\sqrt{2}(2-x)$,
∵AB2+BE2=AE2=EF2,即4+x2=2(2-x)2,解得$x=4-2\sqrt{3}$,
∴$BE+DF=2x=8-4\sqrt{3}$,$EF=\sqrt{2}(2-x)=2\sqrt{6}-2\sqrt{2}≠BE+EF$,${S_{△CEF}}=\frac{1}{2}E{C^2}=\frac{1}{2}{(2-x)^2}=\frac{1}{2}{(2\sqrt{3}-2)^2}=8-4\sqrt{3}$,$2{S_{△ABE}}=AB•BE=2(4-2\sqrt{3})=8-4\sqrt{3}$,
∴S△CEF=2S△ABE,
故选C
点评 此题考查正方形的性质,关键是根据正方形的性质和全等三角形的判定进行分析解答.

练习册系列答案
相关题目
11.已知点A(m,1)与点B(5,n)关于原点对称,则m和n的值为( )
| A. | m=5,n=-1 | B. | m=-5,n=1 | C. | m=-1,n=-5 | D. | m=-5,n=-1 |
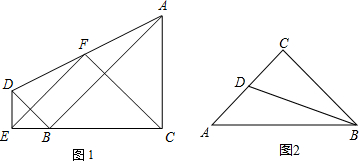
 已知:如图所示,AC⊥AB于点A,BD⊥AB于点B,∠1=∠2,试判断AE与BF的位置关系,并说明理由.
已知:如图所示,AC⊥AB于点A,BD⊥AB于点B,∠1=∠2,试判断AE与BF的位置关系,并说明理由.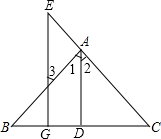 如图,在△ABC中,E是CA延长线上一点,AD⊥BC于D,EG⊥BC于G,∠E=∠3.
如图,在△ABC中,E是CA延长线上一点,AD⊥BC于D,EG⊥BC于G,∠E=∠3.