题目内容
14.若直角三角形的两个锐角的比是2:1,斜边长为8,则它的周长为12+4$\sqrt{3}$.分析 先由直角三角形的两个锐角的比是2:1及直角三角形的两个锐角互余,求出∠B=60°,∠A=30°,再根据含30度角的直角三角形的性质及勾股定理即可解答.
解答  解:如图所示,Rt△ABC中,∠C=90°,∠B:∠A=2:1,斜边AB长为8,
解:如图所示,Rt△ABC中,∠C=90°,∠B:∠A=2:1,斜边AB长为8,
∵∠B+∠A=90°,
∴∠B=60°,∠A=30°,
∴BC=$\frac{1}{2}$AB=$\frac{1}{2}$×8=4,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=4$\sqrt{3}$,
故此三角形的周长是8+4+4$\sqrt{3}$=12+4$\sqrt{3}$.
故答案为12+4$\sqrt{3}$.
点评 本题考查了含30度角的直角三角形的性质:直角三角形中,30°所对的直角边是斜边的一半.也考查了勾股定理及直角三角形的两个锐角互余的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.用配方法解下列方程时,配方正确的是( )
| A. | 方程x2-6x-5=0,可化为(x-3)2=4 | |
| B. | 方程y2-2y-2015=0,可化为(y-1)2=2015 | |
| C. | 方程a2+8a+9=0,可化为(a+4)2=25 | |
| D. | 方程2x2-6x-7=0,可化为${({x-\frac{3}{2}})^2}=\frac{23}{4}$ |
4.在一次函数y=(m-1)x+3的图象上,y随x的增大而减小,则m的取值范围是( )
| A. | m>1 | B. | m>0 | C. | m≥1 | D. | m<1 |
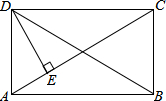 如图,在矩形ABCD中,DE⊥AC,∠ADE=$\frac{1}{2}$∠CDE,那么∠BDC的度数为30°.
如图,在矩形ABCD中,DE⊥AC,∠ADE=$\frac{1}{2}$∠CDE,那么∠BDC的度数为30°.
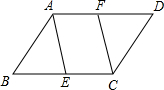 如图,在平行四边形ABCD中,点E、F分别在BC、AD上,且DF=BE.
如图,在平行四边形ABCD中,点E、F分别在BC、AD上,且DF=BE.