题目内容
14.在实数范围内分解因式:x4-4x2+4=${{(x-\sqrt{2})}^{2}(x+\sqrt{2})}^{2}$.分析 先用完全平方公式,再用平方差公式.
解答 解:x4-4x2+4
=(x2-2)2,
=${(x-\sqrt{2})}^{2}$${(x+\sqrt{2})}^{2}$.
故答案为:${{(x-\sqrt{2})}^{2}(x+\sqrt{2})}^{2}$.
点评 本题考查了在实数范围内分解因式.根据因式分解的意义,在实数范围内进行因式分解,其结果必须是几个整式的积.本题关键是运用完全平方公式和平方差公式.

练习册系列答案
相关题目
5.在平面直角坐标系xOy中,第一象限内的点P在反比例函数的图象上,如果点P的纵坐标是3,OP=5,那么该函数的表达式为( )
| A. | y=$\frac{12}{x}$ | B. | y=-$\frac{12}{x}$ | C. | y=$\frac{15}{x}$ | D. | y=-$\frac{15}{x}$ |
2.一个不透明的口袋里有4张形状完全相同的卡片,分别写有数字1,2,3,4,口袋外有两张卡片,分别写有数字2,3,现随机从口袋里取出一张卡片,则两次摸出的卡片的数字之和等于4的概率( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 1 |
9.如果点A(-4,y1),B(-1,y2),C(3,y3)都在反比例函数$y=\frac{k}{x}(k<0)$的图象上,那么y1,y2,y3的大小关系是( )
| A. | y1<y3<y2 | B. | y3<y1<y2 | C. | y1<y2<y3 | D. | y3<y2<y1 |
3.3-1的值等于( )
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
4.下列计算正确的是( )
| A. | $\sqrt{4}$=±2 | B. | 3-1=-$\frac{1}{3}$ | C. | (-1)2015=-1 | D. | |-2|=-2 |

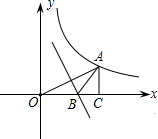 如图,点A(3,m)在双曲线$y=\frac{3}{x}$上,过点A作AC⊥x轴于点C,线段OA的垂直平分线交OC于点B,则△ABC的周长的值为( )
如图,点A(3,m)在双曲线$y=\frac{3}{x}$上,过点A作AC⊥x轴于点C,线段OA的垂直平分线交OC于点B,则△ABC的周长的值为( )