题目内容
19.实数x,y满足|2x-y+1|+2$\sqrt{3x-2y+4}$=0,则代数式$\frac{x-y}{x-2y}$÷$\frac{{x}^{2}-{y}^{2}}{{x}^{2}-4xy+4{y}^{2}}$的值为( )| A. | $\frac{2}{5}$ | B. | -$\frac{8}{7}$ | C. | $\frac{5}{3}$ | D. | -$\frac{4}{5}$ |
分析 原式利用除法法则变形,约分得到最简结果,利用非负数的性质列出方程组,求出方程组的解得到x与y的值,代入原式计算即可得到结果.
解答 解:∵|2x-y+1|+2$\sqrt{3x-2y+4}$=0,
∴$\left\{\begin{array}{l}{2x-y=-1}\\{3x-2y=-4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=2}\\{y=5}\end{array}\right.$,
原式=$\frac{x-y}{x-2y}$•$\frac{(x-2y)^{2}}{(x+y)(x-y)}$=$\frac{x-2y}{x+y}$=$\frac{2-10}{2+5}$=-$\frac{8}{7}$.
故选B.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
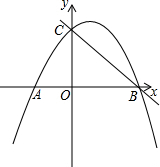 在平面直角坐标系中,点O为坐标原点,直线y=-$\frac{2}{3}$x+6与x轴交于点B,过点B的抛物线y=ax2+bx-27a与直线y=-$\frac{2}{3}$x+6交于y轴上的C点.
在平面直角坐标系中,点O为坐标原点,直线y=-$\frac{2}{3}$x+6与x轴交于点B,过点B的抛物线y=ax2+bx-27a与直线y=-$\frac{2}{3}$x+6交于y轴上的C点.