题目内容
7.直线y=$\frac{5}{3}$x+$\frac{65}{3}$与x轴和y轴的交点分别为A,B,则线段AB上(包括端点A和B)横坐标和纵坐标都是整数的点有5个.分析 分别令x=0求出y的值,y=0时x的值,在线段AB之间找出x的整数值,求出y的对应值,找出x、y均为整数的点即可.
解答 解:令x=0,则y=$\frac{65}{3}$;令y=0,则x=-13,
∴此直线与y轴、x轴的交点分别为:(0,$\frac{65}{3}$)、(-13,0)
当x=0时,y=$\frac{65}{3}$,不符合题意;
当x=-1时,y=20,符合题意;
当x=-2时,y=$\frac{55}{3}$,不符合题意;
当x=-3时,y=-$\frac{50}{3}$,不符合题意;
当x=-4时,y=15,符合题意
当x=-5时,y=$\frac{40}{3}$,不符合题意
当x=-6时,y=$\frac{35}{3}$,不符合题意;
当x=-7时,y=10,符合题意;
当x=-8时,y=$\frac{25}{3}$,不符合题意;
当x=-9时,y=$\frac{20}{3}$,不符合题意;
当x=-10时,y=5,符合题意;
当x=-11时,y=$\frac{10}{3}$,不符合题意;
当x=-12时,y=$\frac{5}{3}$,不符合题意;
当x=-13时,y=0,符合题意;
故答案为5.
点评 本题考查的是一次函数图象上点的坐标特点,解答此题的关键是求出函数图象与两坐标轴的交点,再用列举法找出符合条件的点的坐标.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.(2009-π)0等于( )
| A. | 0 | B. | 1 | C. | 2009 | D. | π |
18.将抛物线y=2(x+l)2向下平移1个单位长度,再向左平移1个单位长度,平移后抛物线的表达式是( )
| A. | y=2(x+2)2-1 | B. | y=2x2-1 | C. | y=2(x+2)2+1 | D. | y=2(x-1)2-1 |
2.如图,在△ABC中,∠ACB=90°,∠B=30°,AC=1,AC在直线l上.将△ABC绕点A顺时针旋转到位置①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+$\sqrt{3}$;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+$\sqrt{3}$;…,按此规律继续旋转,直到得到点P2014为止,则P1P2014=( )
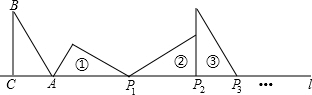

| A. | 2012+671$\sqrt{3}$ | B. | 2013+671$\sqrt{3}$ | C. | 2014+671$\sqrt{3}$ | D. | 2015+671$\sqrt{3}$ |
12.在实数2、0、-1、-$\sqrt{15}$中,最小的实数是( )
| A. | 2 | B. | 0 | C. | -1 | D. | -$\sqrt{15}$ |
19.实数x,y满足|2x-y+1|+2$\sqrt{3x-2y+4}$=0,则代数式$\frac{x-y}{x-2y}$÷$\frac{{x}^{2}-{y}^{2}}{{x}^{2}-4xy+4{y}^{2}}$的值为( )
| A. | $\frac{2}{5}$ | B. | -$\frac{8}{7}$ | C. | $\frac{5}{3}$ | D. | -$\frac{4}{5}$ |