题目内容
14.已知实数x满足x2+$\frac{1}{{x}^{2}}$+x-$\frac{1}{x}$=4,则x-$\frac{1}{x}$的值是1或-2.分析 设x-$\frac{1}{x}$=t,则原方程利用完全平方公式转化为关于t的一元二次方程t2+t+2=4,通过解该方程求得t即x-$\frac{1}{x}$的值.
解答 解:x-$\frac{1}{x}$=t,则由原方程,得
t2+t+2=4,
整理,得
(t-1)(t+2)=0,
解得 t=1或t=-2,
所以 x-$\frac{1}{x}$的值是 1或-2.
故答案是:1或-2.
点评 本题考查了换元法解分式方程.用换元法解一些复杂的分式方程是比较简单的一种方法,根据方程特点设出相应未知数,解方程能够使问题简单化.

练习册系列答案
相关题目
2.如图,在△ABC中,∠ACB=90°,∠B=30°,AC=1,AC在直线l上.将△ABC绕点A顺时针旋转到位置①,可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+$\sqrt{3}$;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+$\sqrt{3}$;…,按此规律继续旋转,直到得到点P2014为止,则P1P2014=( )
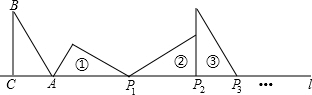

| A. | 2012+671$\sqrt{3}$ | B. | 2013+671$\sqrt{3}$ | C. | 2014+671$\sqrt{3}$ | D. | 2015+671$\sqrt{3}$ |
19.实数x,y满足|2x-y+1|+2$\sqrt{3x-2y+4}$=0,则代数式$\frac{x-y}{x-2y}$÷$\frac{{x}^{2}-{y}^{2}}{{x}^{2}-4xy+4{y}^{2}}$的值为( )
| A. | $\frac{2}{5}$ | B. | -$\frac{8}{7}$ | C. | $\frac{5}{3}$ | D. | -$\frac{4}{5}$ |
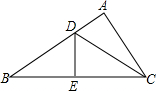 如图,在△ABC中,AB=10cm,AC=6cm,BC的垂直平分线交AB于点D,交BC于点E,则△ACD的周长为16cm.
如图,在△ABC中,AB=10cm,AC=6cm,BC的垂直平分线交AB于点D,交BC于点E,则△ACD的周长为16cm.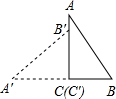 如图,△ABC中,∠ACB=90°,AB=5,AC=4,将△ABC绕点C沿逆时针方向旋转90°得到的△A′B′C′沿CB向右平移,使点B′刚好落在AB边上,则△A′B′C′向右平移的距离是$\frac{3}{4}$.
如图,△ABC中,∠ACB=90°,AB=5,AC=4,将△ABC绕点C沿逆时针方向旋转90°得到的△A′B′C′沿CB向右平移,使点B′刚好落在AB边上,则△A′B′C′向右平移的距离是$\frac{3}{4}$.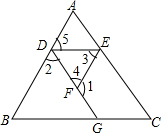 如图所示,已知∠1+∠2=180°,∠3=∠B.
如图所示,已知∠1+∠2=180°,∠3=∠B.