题目内容
18. 如图,已知钝角△ABC
如图,已知钝角△ABC(1)过点A作BC边的垂线,交CB的延长线于点D;(尺规作图,保留作图痕迹,不要求写作法)
(2)在(1)的条件下,若∠ABC=122°,BC=5,AD=4,求CD的长.(结果保留到0.1,参考数据:sin32°=0.53,cos32°=0.85,tan32°=0.62.)
分析 (1)利用基本作图:过直线外一点作直线的垂线作出垂线段AD即可;
(2)根据三角形外角的性质求出∠DAB的度数,在Rt△ADB中,利用锐角三角函数的定义求出DB的长,进而可得出结论.
解答  解:(1)如图所示;
解:(1)如图所示;
(2)∵∠ABC=122°,∠D=90°,
∴∠DAB=32°.
在Rt△ADB中,
∵tan∠DAB=$\frac{DB}{AD}$,即0.62=$\frac{DB}{4}$,
∴DB=2.48,
∴DC=2.48+5=7.48≈7.5.
点评 本题考查的是作图-基本作图,熟知过直线外一点作直线的垂线的作法是解答此题的关键.

练习册系列答案
相关题目
13.下列图形不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
10. 如图,AB∥CD,如果∠A=40°,∠B=20°,那么∠C为( )
如图,AB∥CD,如果∠A=40°,∠B=20°,那么∠C为( )
 如图,AB∥CD,如果∠A=40°,∠B=20°,那么∠C为( )
如图,AB∥CD,如果∠A=40°,∠B=20°,那么∠C为( )| A. | 40° | B. | 60° | C. | 20° | D. | 70° |
 如图,已知线段a,b,c,求作一个三角形ABC,使AB=a,AC=b,BC边上的高AD=c.(不写作法,但要保留作图痕迹)
如图,已知线段a,b,c,求作一个三角形ABC,使AB=a,AC=b,BC边上的高AD=c.(不写作法,但要保留作图痕迹)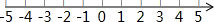 解不等式组$\left\{\begin{array}{l}{2x>4x-6,}&{①}\\{\frac{2x+3}{3}-\frac{1}{2}x≥1,}&{②}\end{array}\right.$,并将它的解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{2x>4x-6,}&{①}\\{\frac{2x+3}{3}-\frac{1}{2}x≥1,}&{②}\end{array}\right.$,并将它的解集在数轴上表示出来.