题目内容
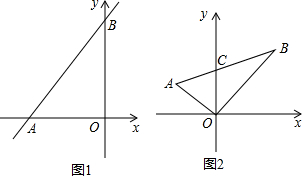 如图1,在平面直角坐标系中,直线AB分别交x轴y轴于A、B两点.设∠OAB=a°,∠OBA=b°,且
如图1,在平面直角坐标系中,直线AB分别交x轴y轴于A、B两点.设∠OAB=a°,∠OBA=b°,且
|
(1)求∠OAB的度数.
(2)将△AOB绕O顺时针旋转30°,至如图2,AB交y轴于点C,求∠AOC的度数.
考点:直角三角形的性质,二元一次方程的解,坐标与图形性质
专题:
分析:(1)根据直角三角形两锐角互余可得a+b=90°,根据二元一次方程的解的定义可得a-2b=0,然后联立方程组求解即可;
(2)根据旋转角的定义列式计算即可得解.
(2)根据旋转角的定义列式计算即可得解.
解答:解:(1)∵∠OAB=a°,∠OBA=b°,且
是方程x-2y=0的一个解,
∴
,
①-②得,3b=90°,
解得b=30°,
把b=30°代入②得,a=60°,
∴∠OAB=60°;
(2)∵△AOB绕O顺时针旋转角度为30°,
∴∠AOC=90°-30°=60°.
|
∴
|
①-②得,3b=90°,
解得b=30°,
把b=30°代入②得,a=60°,
∴∠OAB=60°;
(2)∵△AOB绕O顺时针旋转角度为30°,
∴∠AOC=90°-30°=60°.
点评:本题考查了直角三角形两锐角互余的性质,二元一次方程组的解的定义,坐标与图形性质,难点在于(1)列出关于a、b的二元一次方程组.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 在一次海面搜救行动中,我国的海巡搜救船在某海域的A,B两处探测到C处有疑似飞机黑匣子的脉冲信号,已知A,B两处相距2700米,探测线EC,FC与海平面所在直线GH的夹角分别是32°和45°,试确定疑似脉冲信号所在点C与GH的距离,(精确到0.1米)
在一次海面搜救行动中,我国的海巡搜救船在某海域的A,B两处探测到C处有疑似飞机黑匣子的脉冲信号,已知A,B两处相距2700米,探测线EC,FC与海平面所在直线GH的夹角分别是32°和45°,试确定疑似脉冲信号所在点C与GH的距离,(精确到0.1米)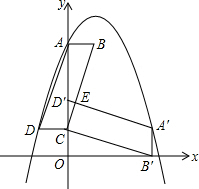 如图,在平面直角坐标系中,?ABCD的顶点A、B、C的坐标分别为A(0,4)、B(1,4)、C(0,1),将?ABCD绕点C沿顺时针方向旋转90°,得到?A′B′CD′,A′D′与BC相交于点E.
如图,在平面直角坐标系中,?ABCD的顶点A、B、C的坐标分别为A(0,4)、B(1,4)、C(0,1),将?ABCD绕点C沿顺时针方向旋转90°,得到?A′B′CD′,A′D′与BC相交于点E.
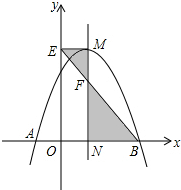 如图,抛物线y=-x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F,已知点A的坐标为(-1,0).
如图,抛物线y=-x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F,已知点A的坐标为(-1,0). 如图,已知两个反比例函数
如图,已知两个反比例函数