题目内容
11.【问题情境】如图1,Rt△ABC中,∠ACB=90°,CD⊥AB,我们可以利用△ABC与△ACD相似证明AC2=AD•AB,这个结论我们称之为射影定理,试证明这个定理;【结论运用】如图2,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,过点C作CF⊥BE,垂足为F,连接OF,
(1)试利用射影定理证明△BOF∽△BED;
(2)若DE=2CE,求OF的长.
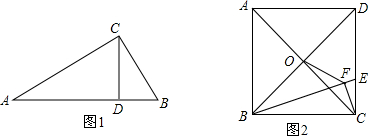
分析 【问题情境】通过证明Rt△ACD∽Rt△ABC得到AC:AB=AD:AC,然后利用比例性质即可得到AC2=AD•AB;
【结论运用】(1)根据射影定理得BC2=BO•BD,BC2=BF•BE,则BO•BD=BF•BE,即$\frac{BO}{BE}$=$\frac{BF}{BD}$,加上∠OBF=∠EBD,于是可根据相似三角形的判定得到△BOF∽△BED;
(2)先计算出DE=4,CE=2,BE=2$\sqrt{10}$,OB=3$\sqrt{2}$,再利用(1)中结论△BOF∽△BED得到$\frac{OF}{DE}$=$\frac{BO}{BE}$,即$\frac{OF}{4}$=$\frac{3\sqrt{2}}{2\sqrt{10}}$,然后利用比例性质求OF.
解答 【问题情境】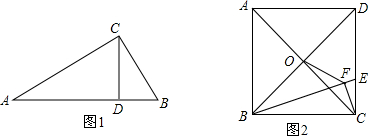
证明:如图1,
∵CD⊥AB,
∴∠ADC=90°,
而∠CAD=∠BAC,
∴Rt△ACD∽Rt△ABC,
∴AC:AB=AD:AC,
∴AC2=AD•AB;
【结论运用】
(1)证明:如图2,
∵四边形ABCD为正方形,
∴OC⊥BO,∠BCD=90°,
∴BC2=BO•BD,
∵CF⊥BE,
∴BC2=BF•BE,
∴BO•BD=BF•BE,
即$\frac{BO}{BE}$=$\frac{BF}{BD}$,
而∠OBF=∠EBD,
∴△BOF∽△BED;
(2)∵BC=CD=6,
而DE=CE,
∴DE=4,CE=2,
在Rt△BCE中,BE=$\sqrt{{2}^{2}+{6}^{2}}$=2$\sqrt{10}$,
在Rt△OBC中,OB=$\frac{\sqrt{2}}{2}$BC=3$\sqrt{2}$,
∵△BOF∽△BED,
∴$\frac{OF}{DE}$=$\frac{BO}{BE}$,即$\frac{OF}{4}$=$\frac{3\sqrt{2}}{2\sqrt{10}}$,
∴OF=$\frac{6\sqrt{5}}{5}$.
点评 本题考查了射影定理:直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项;每一条直角边是这条直角边在斜边上的射影和斜边的比例中项.也考查了相似三角形的判定与性质和正方形的性质.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案| A. | 如果a∥b,a⊥c,那么b⊥c | B. | 如果b∥a,c∥a,那么b∥c | ||
| C. | 如果b⊥a,c⊥a,那么b⊥c | D. | 如果b⊥a,c⊥a,那么b∥c |
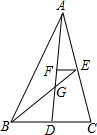 如图,线段AD、BE是△ABC的中线,AD、BE相交于点G,过点E作EF∥BC交AD于点F,若△ABC的面积为12,则△EFG的面积为$\frac{1}{2}$.
如图,线段AD、BE是△ABC的中线,AD、BE相交于点G,过点E作EF∥BC交AD于点F,若△ABC的面积为12,则△EFG的面积为$\frac{1}{2}$.