题目内容
3.计算:①($\frac{1}{2}x$-2y)2;
②(2xy-$\frac{1}{5}$x)2;
③(n+1)2-n2;
④(-2m-n)2;
⑤(x+$\frac{1}{x}$)2;
⑥(x-$\frac{1}{x}$)2;
⑦(a+b+c)2.
分析 原式各项利用完全平方公式化简,计算即可得到结果.
解答 解:①($\frac{1}{2}$x-2y)2=$\frac{1}{4}$x2-2xy+4y2;
②(2xy-$\frac{1}{5}$x)2=4x2y2-$\frac{4}{5}$x2y+$\frac{1}{25}$x2;
③(n+1)2-n2=(n+1+n)(n+1-n)=2n+1;
④(-2m-n)2=4m2+4mn+n2;
⑤(x+$\frac{1}{x}$)2=x2+$\frac{1}{{x}^{2}}$+2;
⑥(x-$\frac{1}{x}$)2=x2+$\frac{1}{{x}^{2}}$-2;
⑦(a+b+c)2=(a+b)2+2c(a+b)+c2=a2+2ab+b2+2ac+2bc+c2.
点评 此题考查了完全平方公式,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
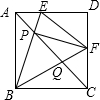 如图,E是正方形ABCD中AD边上的一个动点,AC与BE交于点P,过P点作PF⊥BE交CD边于F点,连结EF、BF,若AB=4,下列结论
如图,E是正方形ABCD中AD边上的一个动点,AC与BE交于点P,过P点作PF⊥BE交CD边于F点,连结EF、BF,若AB=4,下列结论