题目内容
 如图①、②,方格纸中每一个小正方形的边长都为1.求两个图中的格点多边形的面积.
如图①、②,方格纸中每一个小正方形的边长都为1.求两个图中的格点多边形的面积.考点:三角形的面积
专题:网格型
分析:图①用四边形所在的长方形的面积减去四周直角三角形的面积,列式计算即可得解;
图②用四边形所在的长方形的面积减去四周空白部分的面积,列式计算即可得解.
图②用四边形所在的长方形的面积减去四周空白部分的面积,列式计算即可得解.
解答:解:图①,多边形的面积=4×4-
×2×3-
×1×4-
×1×4
=16-3-2-2
=16-7
=9;
图②,多边形的面积=5×4-
×1×4-
×5×2-2×2-
×2×2
=20-2-5-4-2
=20-11
=9.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=16-3-2-2
=16-7
=9;
图②,多边形的面积=5×4-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=20-2-5-4-2
=20-11
=9.
点评:本题考查了三角形的面积,熟练掌握网格结构,准确表示出四边形的面积是解题的关键.

练习册系列答案
相关题目
若一个三角形三个内角度数的比为1:2:3,那么这个三角形最小角的正切值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在四边形ABCD中,AB与CD不平行,E,F分别是AD,BC的中点.求证:EF<
如图,在四边形ABCD中,AB与CD不平行,E,F分别是AD,BC的中点.求证:EF< 某制床厂做了一个每晚睡眠时间的统计,结果如图所示.
某制床厂做了一个每晚睡眠时间的统计,结果如图所示. 如图:已知AC=AD,BC=BD,CE=DE,则全等三角形共有
如图:已知AC=AD,BC=BD,CE=DE,则全等三角形共有
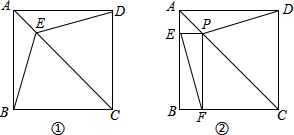 如图①,在正方形ABCD中,点E在AC上.
如图①,在正方形ABCD中,点E在AC上.