题目内容
5.已知x,y满足方程组$\left\{\begin{array}{l}{x-5y=-2}\\{2x+5y=-1}\end{array}\right.$,求代数式(x-y)2-(x+2y)(x-2y)的值.分析 原式利用平方差公式,完全平方公式化简,去括号合并得到最简结果,求出方程组的解得到x与y的值,代入计算即可求出值.
解答 解:原式=(x2-2xy+y2)-(x2-4y2)=x2-2xy+y2-x2+4y2=-2xy+5y2,
方程组$\left\{\begin{array}{l}{x-5y=-2①}\\{2x+5y=-1②}\end{array}\right.$,
①+②得:3x=-3,即x=-1,
把x=-1代入①得:y=$\frac{1}{5}$,
则原式=$\frac{2}{5}$+$\frac{1}{5}$=$\frac{3}{5}$.
点评 此题考查了代数式求值,以及解二元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
15.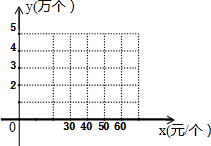 某公司销售一种进价为20(元/个)的计算器,其销售量y(万个)与销售价格x(元/个)的变化如表:
某公司销售一种进价为20(元/个)的计算器,其销售量y(万个)与销售价格x(元/个)的变化如表:
同时,销售过程中的其他开支费用总计40万元.
(1)以x作为点的横坐标,y作为点的纵坐标,把表中的数据,在图中的直角坐标系中描出相应的点,观察顺次连结各点所得的图形,判断y与x的函数关系,并求出y(万个)与x(元/个)的函数解析式.
(2)求出该公司销售这种计算器的净利润w(万元)与销售价格x(元/个)的函数解析式,销售价格定为多少元/个时净利润最大,最大值是多少?
(净利润=销售收入-买入支出-其它开支)
(3)该公司要求净利润不能低于40万元,请写出销售价格x(元/个)的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元/个?
 某公司销售一种进价为20(元/个)的计算器,其销售量y(万个)与销售价格x(元/个)的变化如表:
某公司销售一种进价为20(元/个)的计算器,其销售量y(万个)与销售价格x(元/个)的变化如表:| 价格x(元/个) | … | 30 | 40 | 50 | 60 | … |
| 销售量y(万个) | … | 5 | 4 | 3 | 2 | … |
(1)以x作为点的横坐标,y作为点的纵坐标,把表中的数据,在图中的直角坐标系中描出相应的点,观察顺次连结各点所得的图形,判断y与x的函数关系,并求出y(万个)与x(元/个)的函数解析式.
(2)求出该公司销售这种计算器的净利润w(万元)与销售价格x(元/个)的函数解析式,销售价格定为多少元/个时净利润最大,最大值是多少?
(净利润=销售收入-买入支出-其它开支)
(3)该公司要求净利润不能低于40万元,请写出销售价格x(元/个)的取值范围,若还需考虑销售量尽可能大,销售价格应定为多少元/个?
13. 如图,⊙O的半径为5,点O到直线l的距离为7,点P是直线l上的一个动点,PQ与⊙O相切于点Q,则PQ的最小值为( )
如图,⊙O的半径为5,点O到直线l的距离为7,点P是直线l上的一个动点,PQ与⊙O相切于点Q,则PQ的最小值为( )
 如图,⊙O的半径为5,点O到直线l的距离为7,点P是直线l上的一个动点,PQ与⊙O相切于点Q,则PQ的最小值为( )
如图,⊙O的半径为5,点O到直线l的距离为7,点P是直线l上的一个动点,PQ与⊙O相切于点Q,则PQ的最小值为( )| A. | $\sqrt{17}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{6}$ | D. | 2 |
17. 如图,添加条件不能判断△ACD≌△ABE的是( )
如图,添加条件不能判断△ACD≌△ABE的是( )
 如图,添加条件不能判断△ACD≌△ABE的是( )
如图,添加条件不能判断△ACD≌△ABE的是( )| A. | ∠AEB=∠ADC,CD=BE | B. | AC=AB,AD=AE | C. | AC=AB,∠C=∠B | D. | ∠AEB=∠ADC,∠C=∠B |
14.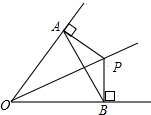 如图所示,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A、B,下列结论不一定成立的是( )
如图所示,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A、B,下列结论不一定成立的是( )
 如图所示,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A、B,下列结论不一定成立的是( )
如图所示,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A、B,下列结论不一定成立的是( )| A. | PA=PB | B. | OA=OB | C. | PO平分∠APB | D. | AB垂直平分OP |
15. 如图,?ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线之和是( )
如图,?ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线之和是( )
 如图,?ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线之和是( )
如图,?ABCD的对角线交于点O,且AB=5,△OCD的周长为23,则?ABCD的两条对角线之和是( )| A. | 18 | B. | 28 | C. | 36 | D. | 46 |
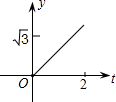
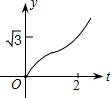
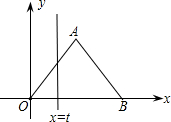 如图,在直角坐标系中,正△AOB的边长为2,设直线x=t(0≤t≤2)截这个三角形所得位于此直线左方的图形的面积为y,则y关于t的函数图象大致是( )
如图,在直角坐标系中,正△AOB的边长为2,设直线x=t(0≤t≤2)截这个三角形所得位于此直线左方的图形的面积为y,则y关于t的函数图象大致是( )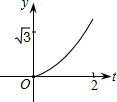
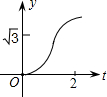
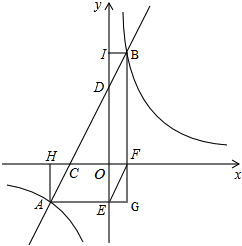 如图,一直线与反比例函数y=$\frac{k}{x}$(k>0)交于A、B两点,直线与x轴、y轴分别交于C、D两点,过A、B两点分别向x轴、y轴作垂线,H、E、F、I为垂足,连接EF,延长AE、BF相交于点G.
如图,一直线与反比例函数y=$\frac{k}{x}$(k>0)交于A、B两点,直线与x轴、y轴分别交于C、D两点,过A、B两点分别向x轴、y轴作垂线,H、E、F、I为垂足,连接EF,延长AE、BF相交于点G.