题目内容
14.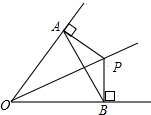 如图所示,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A、B,下列结论不一定成立的是( )
如图所示,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A、B,下列结论不一定成立的是( )| A. | PA=PB | B. | OA=OB | C. | PO平分∠APB | D. | AB垂直平分OP |
分析 由OP平分∠AOB,PA⊥OA,PB⊥OB,根据角平分线的性质,可证得PA=PB,又由等腰三角形的判定,可证得OA=OB,即可判定PO平分∠APB,根据线段垂直平分线的判定,可得OP垂直平分AB.
解答 解:∵OP平分∠AOB,PA⊥OA,PB⊥OB,
∴PA=PB,故A正确;
∴∠PAB=∠PBA,
∵∠OAB=90°-∠PAB,∠OBA=90°-∠PBA,
∴∠OAB=∠OBA,
∴OA=OB,故B正确;
∴PO平分∠APB;故C正确;
∵PA=PB,OA=OB,
∴点P在AB的垂直平分线上,点O在AB的垂直平分线上,
∴OP垂直平分AB,故D错误.
故选D.
点评 此题考查了线段垂直平分线的性质以及角平分线的性质.注意掌握线段垂直平分线的判定的应用是关键.

练习册系列答案
相关题目
9.下列各式属于最简二次根式的是( )
| A. | $\sqrt{18}$ | B. | -$\frac{1}{2}\sqrt{3}$ | C. | $\frac{1}{\sqrt{2}}$ | D. | $\sqrt{\frac{1}{5}}$ |
19.(-2)3的相反数是( )
| A. | -6 | B. | 8 | C. | $-\frac{1}{6}$ | D. | -8 |
6.为了解某市20000名考生的毕业会考数学成绩,从中抽出100名考生的数学成绩进行调查,抽出的100名考生的数学成绩是( )
| A. | 总体 | B. | 样本 | C. | 个体 | D. | 样本容量 |
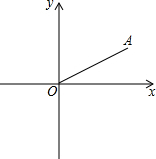 如图,在平面直角坐标系中,点A坐标为(2,1),连接OA,点P是x轴上的一动点,如果△OAP是等腰三角形,请你写出符合条件的点P坐标P1(4,0),P2($\sqrt{5}$,0),P3(-$\sqrt{5}$,0),P4($\frac{5}{4}$,0).
如图,在平面直角坐标系中,点A坐标为(2,1),连接OA,点P是x轴上的一动点,如果△OAP是等腰三角形,请你写出符合条件的点P坐标P1(4,0),P2($\sqrt{5}$,0),P3(-$\sqrt{5}$,0),P4($\frac{5}{4}$,0).