题目内容
16．方程组$\left\{\begin{array}{l}{x+y=4}\\{2x-y=2}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$．分析 方程组利用加减消元法求出解即可．
解答 解：$\left\{\begin{array}{l}{x+y=4①}\\{2x-y=2②}\end{array}\right.$，
①+②得：3x=6，即x=2，
把x=2代入①得：y=2，
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$，
故答案为：$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$
点评 此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
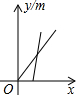
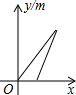
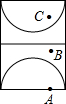在某篮球比赛中，甲队队员A、B的位置如图所示，队员A抢到篮板球后，迅速将球抛向对方半场的点C处，队员B看到后同时快跑到点C处恰好接住了球，则如图中分别表示球、队员B离队员A的距离y（m）与队员A抛球后的时间x的关系的大致图象是（ ）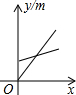
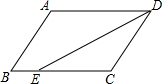已知，如图在?ABCD中，AD=13，AB=10，DE平分∠ADC交BC于点E，则BE=3．
解不等式$\frac{2x-1}{3}-\frac{9x+2}{6}≤1$，把它的解集在数轴上表示出来，并求出这个不等式的负整数解．
如图，将Rt△ABC绕直角顶点A顺时针旋转90°，得到△AB′C′，连结BB′，若∠1=20°，则∠C的度数是65°．