题目内容
16.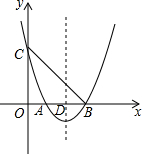 如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
如图,关于x的二次函数y=x2+bx+c的图象与x轴交于点A(1,0)和点B与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使PBC为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
分析 (1)代入A(1,0)和C(0,3),解方程组即可;
(2)求出点B的坐标,再根据勾股定理得到BC,当△PBC为等腰三角形时分三种情况进行讨论:①CP=CB;②BP=BC;③PB=PC.
解答 解:(1)把A(1,0)和C(0,3)代入y=x2+bx+c得:
$\left\{\begin{array}{l}{1+b+c=0}\\{c=3}\end{array}\right.$
解得:b=-4,c=3,
∴二次函数的表达式为:y=x2-4x+3;
(2)令y=0,则x2-4x+3=0,
解得:x=1或x=3,
∴B(3,0),
∴BC=3$\sqrt{2}$,
点P在y轴上,当△PBC为等腰三角形时分三种情况进行讨论:如图所示: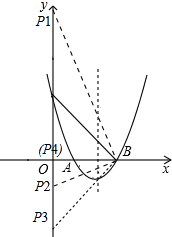
①当CP=CB时,PC=3$\sqrt{2}$,∴OP=OC+PC=3+3$\sqrt{2}$或OP=PC-OC=3$\sqrt{2}$-3
∴P1(0,3+3$\sqrt{2}$),P2(0,3-3$\sqrt{2}$);
②当PB=PC时,OP=OB=3,
∴P3(0,-3);
③当BP=BC时,
∵OC=OB=3
∴此时P与O重合,
∴P4(0,0);
综上所述,点P的坐标为:(0,3+3$\sqrt{2}$)或(0,3-3$\sqrt{2}$)或(0,-3)或(0,0).
点评 本题是二次函数的综合题型,其中涉及到运用待定系数法求二次函数,等腰三角形的性质,运用数形结合、分类讨论及方程思想是解题的关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
18.已知y1=x+1,y2=3x-5.当y1>y2时,x的取值范围是( )
| A. | x>3 | B. | x<3 | C. | x<-3 | D. | x>-3 |
11.下列关系式中,属于二次函数的是(x是自变量)( )
| A. | y=$\frac{1}{3}{x}^{2}$ | B. | y=$\sqrt{{x}^{2}-1}$ | C. | y=$\frac{1}{{x}^{2}}$ | D. | y=ax2+bx+c |
8. 图中几何体的截面的形状图是( )
图中几何体的截面的形状图是( )
 图中几何体的截面的形状图是( )
图中几何体的截面的形状图是( )| A. |  | B. |  | C. |  | D. |  |
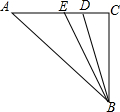 如图,在Rt△ABC中,∠C=90°,∠A=45°,BE是△ABD的角平分线,若∠DBC=15°,则∠EBD的度数为7.5°.
如图,在Rt△ABC中,∠C=90°,∠A=45°,BE是△ABD的角平分线,若∠DBC=15°,则∠EBD的度数为7.5°.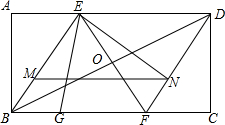 已知如图,矩形ABCD的对角线BD的中垂线分别交AD、BC边于点E、F,连结EB、DF.AB=$\sqrt{3}$,AD=3.
已知如图,矩形ABCD的对角线BD的中垂线分别交AD、BC边于点E、F,连结EB、DF.AB=$\sqrt{3}$,AD=3.