题目内容
当点A(1,2),B(3,-3),C(m,n)三点可以确定一个圆时,m,n需要满足的条件 .
考点:确定圆的条件,坐标与图形性质
专题:
分析:能确定一个圆就是不在同一直线上,首先确定直线AB的解析式,然后点C不满足求得的直线即可.
解答:解:设直线AB的解析式为y=kx+b,
∵A(1,2),B(3,-3),
∴
解得:k=-
,b=
,
∴直线AB的解析式为y=-
x+
,
∵点A(1,2),B(3,-3),C(m,n)三点可以确定一个圆时,
∴点C不在直线AB上,
∴5m+2n≠9,
故答案为:5m+2n≠9.
∵A(1,2),B(3,-3),
∴
|
解得:k=-
| 5 |
| 2 |
| 9 |
| 2 |
∴直线AB的解析式为y=-
| 5 |
| 2 |
| 9 |
| 2 |
∵点A(1,2),B(3,-3),C(m,n)三点可以确定一个圆时,
∴点C不在直线AB上,
∴5m+2n≠9,
故答案为:5m+2n≠9.
点评:本题考查了确定圆的条件及坐标与图形的性质,能够了解确定一个圆时三点不共线是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 彼此相似的矩形A1B1C1D1,A2B2C2D2,A3B3C3D3,…,按如图所示的方式放置.点A1,A2,A3,…,和点C1,C2,C3,…,分别在直线y=kx+b(k>0)和x轴上,已知点B1、B2的坐标分别为(1,2),(3,4),则Bn的坐标是( )
彼此相似的矩形A1B1C1D1,A2B2C2D2,A3B3C3D3,…,按如图所示的方式放置.点A1,A2,A3,…,和点C1,C2,C3,…,分别在直线y=kx+b(k>0)和x轴上,已知点B1、B2的坐标分别为(1,2),(3,4),则Bn的坐标是( )| A、(2n-1,2n) | ||
B、(2n-
| ||
C、(2n-1-
| ||
| D、(2n-1-1,2n-1) |
 如图,M为双曲线y=
如图,M为双曲线y= 如图,圆柱形容器中,高为120cm,底面周长为100cm,在容器内壁离容器底部40cm的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿40cm与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为
如图,圆柱形容器中,高为120cm,底面周长为100cm,在容器内壁离容器底部40cm的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿40cm与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为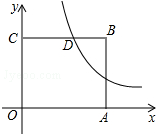 如图,在平面直角坐标系中,正方形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(4,4),反比例函数的图象经过CB的中点D,若点P(x,y)在该反比例函数的图象上运动(不与点D重合),过点P作PR⊥y轴于点R,作PQ⊥BC所在直线于点Q,记四边形CQPR的面积为S=4时,x的值为
如图,在平面直角坐标系中,正方形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(4,4),反比例函数的图象经过CB的中点D,若点P(x,y)在该反比例函数的图象上运动(不与点D重合),过点P作PR⊥y轴于点R,作PQ⊥BC所在直线于点Q,记四边形CQPR的面积为S=4时,x的值为 如图,四边形ABCD是正方形,AE、CF分别垂直于过顶点B的直线l,垂足分别为E、F.求证:BE=CF.
如图,四边形ABCD是正方形,AE、CF分别垂直于过顶点B的直线l,垂足分别为E、F.求证:BE=CF.