题目内容
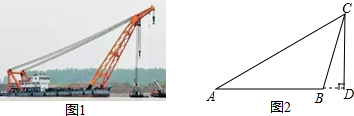
10.如图1是“东方之星”救援打捞现场图,小红据此构造出一个如图2所示的数学模型,已知:A、B、D三点在同一水平线上,CD⊥AD,∠A=30°,∠CBD=75°,AB=60m.(1)求点B到AC的距离;
(2)求线段CD的长度.
分析 过点B作BE⊥AC于点E,在直角三角形AEB中,利用锐角三角函数定义求出AE的长,在直角三角形CEB中,利用锐角三角函数定义求出BE与CE的长,由AE+CE求出AC的长,即可求出CD的长.
解答 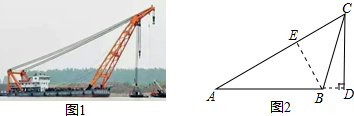 解:过点B作BE⊥AC于点E,
解:过点B作BE⊥AC于点E,
在Rt△AEB中,AB=60m,sinA=$\frac{1}{2}$,BE=ABsinA=60×$\frac{1}{2}$=30,cosA=$\frac{AE}{AB}$,
∴AE=60×$\frac{\sqrt{3}}{2}$=30$\sqrt{3}$m,
在Rt△CEB中,∠ACB=∠CBD-∠A=75°-30°=45°,
∴BE=CE=30m,
∴AC=AE+CE=(30+30$\sqrt{3}$)m,
在Rt△ADC中,sinA=$\frac{CD}{AC}$,
则CD=(30+30$\sqrt{3}$)×$\frac{1}{2}$=(15+15$\sqrt{3}$)m.
点评 此题考查了解直角三角形的应用,熟练掌握锐角三角函数定义是解本题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
20.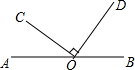 如图,点O在直线AB上,且OC⊥OD,若∠DOB=46°,则∠COA的大小是( )
如图,点O在直线AB上,且OC⊥OD,若∠DOB=46°,则∠COA的大小是( )
 如图,点O在直线AB上,且OC⊥OD,若∠DOB=46°,则∠COA的大小是( )
如图,点O在直线AB上,且OC⊥OD,若∠DOB=46°,则∠COA的大小是( )| A. | 34° | B. | 44° | C. | 54° | D. | 64° |
18.下列运算正确的是( )
| A. | x2•x3=x6 | B. | 5x-2x=3x | C. | (x2)3=x5 | D. | (-2x)2=-4x2 |
15.下列说法中,正确的是( )
| A. | -$\frac{3}{4}$x2的系数是$\frac{3}{4}$ | B. | $\frac{3}{2}$πa2的系数是$\frac{3}{2}$ | C. | 3ab2的系数是3a | D. | $\frac{2}{5}$xy2的系数是$\frac{2}{5}$ |
2.已知点A(a,1)与B(-2,b)关于坐标原点对称,那么点P(a,b)绕原点顺时针旋转90°后的对应点P′的坐标是( )
| A. | (-1,2) | B. | (1,-2) | C. | (-1,-2) | D. | (1,2) |
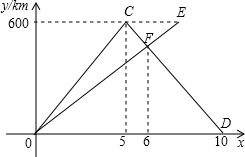 甲,乙两车同时从A城出发驶往B城,甲车到达B城后立即按原速返回A城,乙车继续行驶到B城,下面的图象反映的过程是离A城的距离y(km)与甲车行驶时间x(h)之间的函数关系.
甲,乙两车同时从A城出发驶往B城,甲车到达B城后立即按原速返回A城,乙车继续行驶到B城,下面的图象反映的过程是离A城的距离y(km)与甲车行驶时间x(h)之间的函数关系.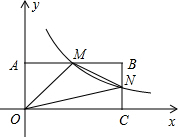 如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线y=-$\frac{1}{2}$x+3交AB,BC分别于点M,N,反比例函数y=$\frac{k}{x}$的图象经过点M,N.
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线y=-$\frac{1}{2}$x+3交AB,BC分别于点M,N,反比例函数y=$\frac{k}{x}$的图象经过点M,N.