题目内容
5.不等式组$\left\{\begin{array}{l}{4x-2≤3x}\\{2x+5>3}\end{array}\right.$的解集为-1<x≤2.分析 先求出每个不等式的解集,再根据不等式的解集找出不等式组的解集即可.
解答 解:$\left\{\begin{array}{l}{4x-2≤3x①}\\{2x+5>3②}\end{array}\right.$
∵解不等式①得:x≤2,
解不等式②得:x>-1,
∴不等式组的解集为-1<x≤2,
故答案为:-1<x≤2.
点评 本题考查了解一元一次不等式组的应用,解此题的关键是能根据不等式的解集找出不等式组的解集,难度适中.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
13.二元一次方程3x-2y=1的不超过10的正整数解共有( )组.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
20.任意大于1的正整数m的三次幂均可“分裂”成m个连续奇数的和,如:23=3+5,33=7+9+11,43=13+15+17+19,…按此规律,若m3分裂后其中有一个奇数是2015,则m的值是( )
| A. | 46 | B. | 45 | C. | 44 | D. | 43 |
17. 如图,已知AB∥CD,若∠A=25°,∠E=40°,则∠C等于( )
如图,已知AB∥CD,若∠A=25°,∠E=40°,则∠C等于( )
 如图,已知AB∥CD,若∠A=25°,∠E=40°,则∠C等于( )
如图,已知AB∥CD,若∠A=25°,∠E=40°,则∠C等于( )| A. | 40° | B. | 65° | C. | 115° | D. | 25° |
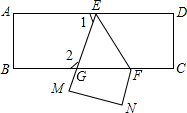 把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=55°,求:
把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=55°,求: