题目内容
11. 如图所示,△ABC是等腰直角三角形,AB=AC,D是斜边BC的中点,E、F分别是AB、AC边上的点,且DE⊥DF,若BE=12,CF=5.
如图所示,△ABC是等腰直角三角形,AB=AC,D是斜边BC的中点,E、F分别是AB、AC边上的点,且DE⊥DF,若BE=12,CF=5.(1)求线段EF的长;
(2)求四边形AFDE面积.
分析 (1)首先连接AD,由△ABC是等腰直角三角形,AB=AC,D是斜边BC的中点,可得:AD=DC,∠EAD=∠C=45°,AD⊥BC,即∠CDF+∠ADF=90°,又DE⊥DF,可得:∠EDA+∠ADF=90°,故∠EDA=∠CDF,从而可证:△AED≌△CFD;根据全等三角形的性质得到AE=CF=5,进而得出BE=AF=12.然后在Rt△AEF中,运用勾股定理可将EF的值求出;
(2)由(1)知△AED≌△CFD,根据全等三角形的面积相等得出S四边形AFDE=S△ADC=$\frac{1}{2}$S△ABC,根据三角形的面积公式计算即可.
解答 解:(1)连接AD.
∵△ABC是等腰直角三角形,AB=AC,D是斜边BC的中点,
∴AD=DC=DB,AD⊥BC,
∴∠BAD=∠C=45°,
∵∠EDA+∠ADF=90°,
又∵∠CDF+∠ADF=90°,
∴∠EDA=∠CDF.
在△AED与△CFD中,
$\left\{\begin{array}{l}{∠EDA=∠FDC}\\{AD=CD}\\{∠EAD=∠C}\end{array}\right.$,
∴△AED≌△CFD(ASA).
∴AE=CF=5.  ∵AB=AC,
∵AB=AC,
∴BE=AF=12.
在Rt△AEF中,∵∠EAF=90°,
∴EF2=AE2+AF2=52+122=169,
∴EF=13;
(2)由(1)知△AED≌△CFD,
所以S四边形AFDE=S△AFD+S△AED
=S△AFD+S△CFD
=S△ADC
=$\frac{1}{2}$S△ABC
=$\frac{1}{2}$×$\frac{1}{2}$AB2
=$\frac{1}{4}$(12+5)2
=$\frac{289}{4}$.
点评 本题考查了等腰直角三角形的性质,直角三角形斜边上的中线的性质,全等三角形的判定与性质,三角形的面积,本题中求证△ADE≌△CDF是解题的关键.

 英才计划期末调研系列答案
英才计划期末调研系列答案 如图,点O为直线AB上一点,OC⊥OD,若∠1=35°,则∠2的度数是( )
如图,点O为直线AB上一点,OC⊥OD,若∠1=35°,则∠2的度数是( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
 如图,已知∠AOB=70°,OC平分∠AOB,DC∥OB,则∠C为( )
如图,已知∠AOB=70°,OC平分∠AOB,DC∥OB,则∠C为( )| A. | 20° | B. | 35° | C. | 45° | D. | 70° |
| 项目 | 第一次锻炼 | 第二次锻炼 |
| 步数(步) | 10000 | ①10000(1+3x) |
| 平均步长(米/步) | 0.6 | ②0.6(1-x) |
| 距离(米) | 6000 | 7020 |
(1)根据题意完成表格填空;
(2)求x;
(3)王老师发现好友中步数排名第一为24000步,因此在两次锻炼结束后又走了500米,使得总步数恰好为24000步,求王老师这500米的平均步长.
 如图,△ABC中,AB=AC,AD是中线,若∠BAD=20°,则∠C的度数为70°.
如图,△ABC中,AB=AC,AD是中线,若∠BAD=20°,则∠C的度数为70°. 矩形定义,有一个角是直角的平行四边形是矩形.
矩形定义,有一个角是直角的平行四边形是矩形.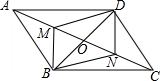 如图,在平行四边形ABCD中,M、N分别是OA,OC的中点,O为对角线AC与BD的交点,试问四边形BMDN是平行四边形吗?说说你的理由.
如图,在平行四边形ABCD中,M、N分别是OA,OC的中点,O为对角线AC与BD的交点,试问四边形BMDN是平行四边形吗?说说你的理由. 如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24cm,△OAB的周长是18cm,则EF=3cm.
如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24cm,△OAB的周长是18cm,则EF=3cm.