题目内容
15.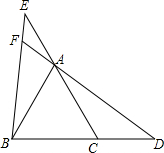 如图,△ABC是等边三角形,点D、E分别是BC、CA延长线上的点,且CD=AE,DA的延长线交BE于点F.
如图,△ABC是等边三角形,点D、E分别是BC、CA延长线上的点,且CD=AE,DA的延长线交BE于点F.(1)求证:△ABE≌△CAD;
(2)求∠BFD的度数.
分析 (1)由△ABC是等边三角形,得到∠BAC=∠ACB=60°,AC=AB,于是得到∠EAB=∠ACD=120°,即可得到结论;
(2)由全等三角形的性质得到∠E=∠D,由于∠D+∠CAD=∠ACB=60°,即可得到结论.
解答 (1)证明:∵△ABC是等边三角形,
∴∠BAC=∠ACB=60°,AC=AB,
∴∠EAB=∠ACD=120°,
在△CAD和△ABE中,
$\left\{\begin{array}{l}{CA=AB}\\{∠ACD=∠BAE}\\{CD=AE}\end{array}\right.$,
∴△ABE≌△CAD;
(2)解:∵△ABE≌△CAD,
∴∠E=∠D,
∵∠D+∠CAD=∠ACB=60°,
∴∠AFB=∠E+∠EAF=∠D+∠CAD=60°.
点评 本题考查了全等三角形的判定和性质,等边三角形的性质,三角形外角的性质,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在△ABC中,AB=AC=2,∠A=90°,点P为BC的中点,点E、F分别为边AB、AC上的点,若∠EPF=45°,∠FEP=60°,则CF=3-$\sqrt{3}$.
如图,在△ABC中,AB=AC=2,∠A=90°,点P为BC的中点,点E、F分别为边AB、AC上的点,若∠EPF=45°,∠FEP=60°,则CF=3-$\sqrt{3}$.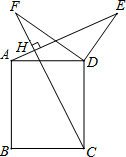 如图,四边形ABCD是矩形,点E和点F是矩形ABCD外两点,AE⊥CF于点H,AD=3,CD=4,DE=2.5,∠EDF=90°,则DF长是$\frac{10}{3}$.
如图,四边形ABCD是矩形,点E和点F是矩形ABCD外两点,AE⊥CF于点H,AD=3,CD=4,DE=2.5,∠EDF=90°,则DF长是$\frac{10}{3}$.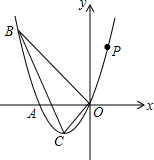 如图,已知抛物线经过点A(-2,0),点B(-3,3)及原点O,顶点为C.
如图,已知抛物线经过点A(-2,0),点B(-3,3)及原点O,顶点为C.