Question

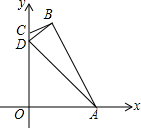如图，四边形ABCD的点A在x轴上，边CD在y轴上，已知A（3，0），B（1，4），D（0，3）．
（1）△ABD的形状是

 

；
（2）在x轴上存在一点P，使以O，D，P为顶点的三角形与△ABD相似，求出点P的坐标；
（3）若tan∠CBD=

1

3

，
①求证：BC是△ABD外接圆的切线；
②求出点C的坐标．

Answer 1

考点：圆的综合题

专题：

分析：（1）过B作BE⊥x轴，交x轴于点E，则可知BE=DE，且OA=OD，可求得∠BDA=90°，可得△ABD为直角三角形；
（2）设P点坐标为（x，0），则OP=|x|，当△ODP和△ABD相似时，则有

AD

OP

=

BD

OD

或

AD

OD

=

BD

OP

，代入计算可求得x的值，可求出P点坐标；
（3）①由BD=

2

，AD=3

2

可得tan∠BAD=

1

3

，可得∠CBD=∠BAD，可得出∠CBD+∠DBA=90°，可证得BC为切线；②由∠CBE=∠DBE-∠DBC，可求得tan∠CBE=

1

2

，可求得CE=

1

2

，则可求得OC的长，从而可得出点C的坐标．

解答：（1）解：
如图，过点B作BE⊥x轴，交x轴于点E，
∵A（3，0），B（1，4），D（0，3），
∴BE=1，OE=4，OD=OA=3，
∴BE=DE=1，
∴∠BDE=∠ODA=45°，
∴∠BDA=90°，
∴△ABD为直角三形，
故答案为：直角三角形；
（2）解：设P点坐标为（x，0），则OP=|x|，
由（1）可求得AD=3

2

，BD=

2

，
∵△ODP和△ABD相似，
∴有

AD

OP

=

BD

OD

或

AD

OD

=

BD

OP

，
当

AD

OP

=

BD

OD

时，有

3 2

|x|

=

2

3

，解得x=±9，此时P点坐标为（9，0）或（-9，0）；
当

AD

OD

=

BD

OP

时，有

2

|x|

=

3 2

3

，解得x=±1，此时P点坐标为（1，0）或（-1，0）；
综上可知P点坐标为（9，0）或（-9，0）或（1，0）或（-1，0）；
（3）①证明：
∵AD=3

2

，BD=

2

，
∴tan∠BAD=

BD

AD

=

1

3

，且tan∠CBD=

1

3

，
∴∠BAD=∠CBD，
∵∠BAD+∠DBA=90°，
∴∠CBD+∠DBA=90°，即∠ABC=90°，
∴AB⊥BC，
∴BC为△ABD外接圆的切线；
②解：∵∠CBE=∠DBE-∠DBC，
∴tan∠CBE=tan（∠DBE-∠DBC）=

tan∠DBE-tan∠DBC

1+tan∠DBE•tan∠DBC

=

1- 1 3

1+ 1 3

=

1

2

，
在Rt△CBE中，tan∠CBE=

CE

BE

，
∴

CE

1

=

1

2

，
∴CE=

1

2

，
∴OC=OE-CE=4-

1

2

=

7

2

，
∴C点坐标为（0，

7

2

）．

点评：本题主要考查相似三角形的性质和切线的判定、三角函数的定义、勾股定理等知识的综合应用．当知道点的坐标时，可利用勾股定理计算出线段的长度，这是解决解析几何常用的方法；在求（2）中P点的坐标时分两种情况是关键；在（3）①中利用求得三角函数相等得到角相等是关键，在②中利用条件求得tan∠CBE=

1

2

是解题的关键．