题目内容
在直角△ABC中，∠C=90°，且3BC=4AC，AB=10，分别求BC、AC的长．
考点：勾股定理
专题：
分析：先根据3BC=4AC设设BC=4k，则AC=3k，根据勾股定理求出k的值，进而可得出BC、AC的长．
解答：解：∵在直角△ABC中，∠C=90°，且3BC=4AC，
∴设BC=4k，则AC=3k，
∴（4k）2+（3k）2=（10）2，解得k2=4，即k=2
∴BC=8，AC=6．
∴设BC=4k，则AC=3k，
∴（4k）2+（3k）2=（10）2，解得k2=4，即k=2
∴BC=8，AC=6．
点评：本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
相关题目
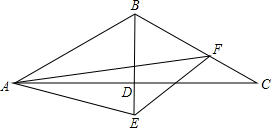已知，△ABC中，BA=BC，∠ABC=120°，BE⊥AC，垂足D，AF平分∠BAE交BC于F．求证：∠AFE=30°．
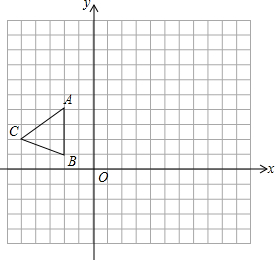如图，在平面直角坐标系xOy中，△ABC三个顶点坐标分别为A（-2，4），B（-2，1），C（-5，2）．
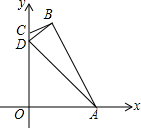如图，四边形ABCD的点A在x轴上，边CD在y轴上，已知A（3，0），B（1，4），D（0，3）．