题目内容
 已知,△ABC的面积为1,D为BC的中点.E、F分别在AC、AB上,且S△BDF=
已知,△ABC的面积为1,D为BC的中点.E、F分别在AC、AB上,且S△BDF=| 1 |
| 5 |
| 1 |
| 3 |
考点:面积及等积变换
专题:
分析:由△ABC的面积为1,可得
BC•h=1,结合D为BC的中点,S△CDE=
,得出AE与CE的关系,同理得出AF与BF的关系.可得出S△AEF,即可得出S△DEF=的值.
| 1 |
| 2 |
| 1 |
| 3 |
解答:解:∵△ABC的面积为1,
∴
BC•h=1,
∵D为BC的中点,S△CDE=
,
∴
×(
BC)•h′=
,
∴h:h′=3:2,
∴AE:CE=1:2,
同理AF:BF=3:2,
S△AEF=
×
×S△ABC=
,
∴S△DEF=1-S△BDF-S△CDE-S△AEF=1-
-
-
=
.
∴
| 1 |
| 2 |
∵D为BC的中点,S△CDE=
| 1 |
| 3 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
∴h:h′=3:2,
∴AE:CE=1:2,
同理AF:BF=3:2,
S△AEF=
| 1 |
| 3 |
| 3 |
| 5 |
| 1 |
| 5 |
∴S△DEF=1-S△BDF-S△CDE-S△AEF=1-
| 1 |
| 5 |
| 1 |
| 3 |
| 1 |
| 5 |
| 4 |
| 15 |
点评:本题主要考查了面积及等积变换,解题的关键是利用中点及面积找出AE与CE之间的关系及AF与BF的关系.

练习册系列答案
相关题目
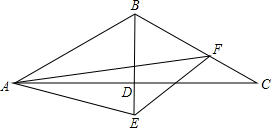 已知,△ABC中,BA=BC,∠ABC=120°,BE⊥AC,垂足D,AF平分∠BAE交BC于F.求证:∠AFE=30°.
已知,△ABC中,BA=BC,∠ABC=120°,BE⊥AC,垂足D,AF平分∠BAE交BC于F.求证:∠AFE=30°.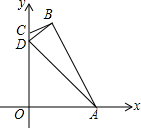 如图,四边形ABCD的点A在x轴上,边CD在y轴上,已知A(3,0),B(1,4),D(0,3).
如图,四边形ABCD的点A在x轴上,边CD在y轴上,已知A(3,0),B(1,4),D(0,3).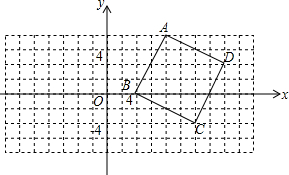 如图,正方形ABCD的顶点坐标分别为A(8,8),B(4,0),C(12,-4),D(16,4),以点O为位似中心,在平面直角坐标系内画出正方形A1B1C1D1,使正方形A1B1C1D1与正方形ABCD的位似比为1:2,并写出点的坐标.
如图,正方形ABCD的顶点坐标分别为A(8,8),B(4,0),C(12,-4),D(16,4),以点O为位似中心,在平面直角坐标系内画出正方形A1B1C1D1,使正方形A1B1C1D1与正方形ABCD的位似比为1:2,并写出点的坐标.