题目内容
 等边三角形ABC中,AD是高,∠ABC的平分线BH交AD于点O,E是AC边上的点,F是BC边上的点,且△OEF为等边三角形
等边三角形ABC中,AD是高,∠ABC的平分线BH交AD于点O,E是AC边上的点,F是BC边上的点,且△OEF为等边三角形(1)求证:△BDO≌△AHO;
(2)△CEF是等边三角形吗?为什么?
考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:(1)根据等边三角形三线合一的性质即可证明AH=BD,即可证明△BDO≌△AHO;
(2)根据(1)中结论可得OD=OH,进而可以证明△ODF≌△OHE,即可证明DF=HE,即可证明△CEF为等边三角形.
(2)根据(1)中结论可得OD=OH,进而可以证明△ODF≌△OHE,即可证明DF=HE,即可证明△CEF为等边三角形.
解答:解:(1)∵等边三角形三线合一,
∴H,D为AC,BC中点,且AD⊥BC,BH⊥AC,BH平分∠ABC,AD平分∠BAC,
∴∠ABO=∠BAO,BD=AH,
∴AO=BO.
RT△OBD和RT△OAH中,
,
∴RT△OBD≌RT△OAH;(HL)
(2)∵RT△OBD≌RT△OAH,
∴OD=OH,
∵等边△OEF中,OE=OF,
在RT△ODF和RT△OHE中,
,
∴RT△ODF≌RT△OHE(HL),
∴DF=HE,
∴CE=CF,
∵∠C=60°,
∴△CEF是等边三角形.
∴H,D为AC,BC中点,且AD⊥BC,BH⊥AC,BH平分∠ABC,AD平分∠BAC,
∴∠ABO=∠BAO,BD=AH,
∴AO=BO.
RT△OBD和RT△OAH中,
|
∴RT△OBD≌RT△OAH;(HL)
(2)∵RT△OBD≌RT△OAH,
∴OD=OH,
∵等边△OEF中,OE=OF,
在RT△ODF和RT△OHE中,
|
∴RT△ODF≌RT△OHE(HL),
∴DF=HE,
∴CE=CF,
∵∠C=60°,
∴△CEF是等边三角形.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证RT△OBD≌RT△OAH是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
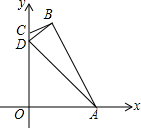 如图,四边形ABCD的点A在x轴上,边CD在y轴上,已知A(3,0),B(1,4),D(0,3).
如图,四边形ABCD的点A在x轴上,边CD在y轴上,已知A(3,0),B(1,4),D(0,3).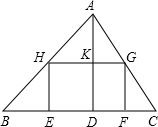 △ABC为锐角三角形,AD是边BC上的高,正方形EFGH的一边EF在BC上,顶点G,H分别在AC,AB上,BC=30,AD=20.求这个正方形的边长.
△ABC为锐角三角形,AD是边BC上的高,正方形EFGH的一边EF在BC上,顶点G,H分别在AC,AB上,BC=30,AD=20.求这个正方形的边长.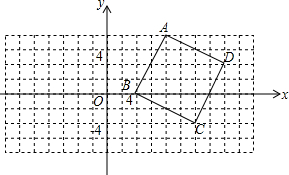 如图,正方形ABCD的顶点坐标分别为A(8,8),B(4,0),C(12,-4),D(16,4),以点O为位似中心,在平面直角坐标系内画出正方形A1B1C1D1,使正方形A1B1C1D1与正方形ABCD的位似比为1:2,并写出点的坐标.
如图,正方形ABCD的顶点坐标分别为A(8,8),B(4,0),C(12,-4),D(16,4),以点O为位似中心,在平面直角坐标系内画出正方形A1B1C1D1,使正方形A1B1C1D1与正方形ABCD的位似比为1:2,并写出点的坐标.