题目内容
用配方法解方程2x2-x-15=0的解是 .
考点:解一元二次方程-配方法
专题:
分析:移项、然后二次项系数化成1,配方、根据平方根的定义转化为两个一元一次方程,即可求解.
解答:解:移项,得:2x2-x=15,
系数化成1得:x2-
x=
,
配方,x2-
x+
=
+
,
即(x-
)2=
,
则x-
=±
,
解得:x1=3,x2=-
.
故答案是:x1=3,x2=-
.
系数化成1得:x2-
| 1 |
| 2 |
| 15 |
| 2 |
配方,x2-
| 1 |
| 2 |
| 1 |
| 16 |
| 15 |
| 2 |
| 1 |
| 16 |
即(x-
| 1 |
| 4 |
| 121 |
| 16 |
则x-
| 1 |
| 4 |
| 11 |
| 4 |
解得:x1=3,x2=-
| 5 |
| 2 |
故答案是:x1=3,x2=-
| 5 |
| 2 |
点评:本题考查了配方法解方程,配方法的一般步骤:
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.

练习册系列答案
相关题目
下列命题中,错误的是( )
| A、三角形两边之差小于第三边 |
| B、三角形的外角和是360° |
| C、三角形的一边中线能将三角形分成面积相等的两部分 |
| D、正多边形都是中心对称图形 |
下列说法正确的是( )
| A、两条直线被第三条直线所截,同位角相等 |
| B、到直线l距离相等的两点关于l对称 |
| C、三角形的三个内角中最小角不大于60° |
| D、三角形的三条高交于三角形内部 |
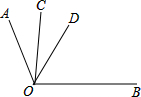 如图,射线OC,OD在∠AOB的内部,OC是∠AOD的平分线,若∠AOB=100°,∠COD=15°,则∠BOD的度数为( )
如图,射线OC,OD在∠AOB的内部,OC是∠AOD的平分线,若∠AOB=100°,∠COD=15°,则∠BOD的度数为( )| A、85° | B、80° |
| C、70° | D、60° |
 如图所示,AB是⊙O的直径,过点A作AC交⊙O于D,且AD=CD,连接BC,过D点作⊙O的切线交BC于E.
如图所示,AB是⊙O的直径,过点A作AC交⊙O于D,且AD=CD,连接BC,过D点作⊙O的切线交BC于E.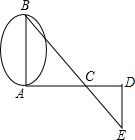 在一次数学活动课上,为了测量河宽AB,其同学采用了如下方法:如图,从A处沿与AB垂直的直线方向走40m到达C处,插一杞标杆,然后沿同方向继续走20m到达D处,再右转90°走到E处,使B,C,E三点恰好在一条直线上,测得DE=30m,这样就可以求出河宽AB,请你算出结果.
在一次数学活动课上,为了测量河宽AB,其同学采用了如下方法:如图,从A处沿与AB垂直的直线方向走40m到达C处,插一杞标杆,然后沿同方向继续走20m到达D处,再右转90°走到E处,使B,C,E三点恰好在一条直线上,测得DE=30m,这样就可以求出河宽AB,请你算出结果.