题目内容
19.先化简,再求值:($\frac{5}{x-2}$-x-2)÷$\frac{{x}^{2}-6x+9}{{x}^{2}-2x}$+$\frac{3x}{x-3}$,其中x=2cos60°+3tan45°.分析 先化简题目中的式子,然后将x的值代入化简后的式子即可解答本题.
解答 解:($\frac{5}{x-2}$-x-2)÷$\frac{{x}^{2}-6x+9}{{x}^{2}-2x}$+$\frac{3x}{x-3}$
=$\frac{5-(x+2)(x-2)}{x-2}×\frac{x(x-2)}{(x-3)^{2}}+\frac{3x}{x-3}$
=$\frac{5-{x}^{2}+4}{(x-3)^{2}}•x+\frac{3x}{x-3}$
=$\frac{-x(x+3)(x-3)}{(x-3)^{2}}+\frac{3x}{x-3}$
=$\frac{-x(x+3)}{x-3}+\frac{3x}{x-3}$
=$\frac{-{x}^{2}}{x-3}$,
当x=2cos60°+3tan45°=2×$\frac{1}{2}+3×1$=4,
原式=$\frac{-{4}^{2}}{4-3}$=-16.
点评 本题考查分式的化简求值,解题的关键是明确分式化简求值的方法.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
14. 如图,AD是∠EAC的平分线,AD∥BC,∠B=40°,则∠C的度数为( )
如图,AD是∠EAC的平分线,AD∥BC,∠B=40°,则∠C的度数为( )
 如图,AD是∠EAC的平分线,AD∥BC,∠B=40°,则∠C的度数为( )
如图,AD是∠EAC的平分线,AD∥BC,∠B=40°,则∠C的度数为( )| A. | 50° | B. | 40° | C. | 30° | D. | 20° |
 跳绳时,绳甩到最高处时的形状是抛物线.正在甩绳的甲、乙两名同学拿绳的手间距AB为6米,到地面的距离AO和BD均为0.9米,身高为1.4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E.以点O为原点建立如图所示的平面直角坐标系,设此抛物线的解析式为y=ax2+bx+0.9.
跳绳时,绳甩到最高处时的形状是抛物线.正在甩绳的甲、乙两名同学拿绳的手间距AB为6米,到地面的距离AO和BD均为0.9米,身高为1.4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E.以点O为原点建立如图所示的平面直角坐标系,设此抛物线的解析式为y=ax2+bx+0.9. 将下列各数在数轴上表示出来,并按从小到大的顺序并用“<”号连接起来:
将下列各数在数轴上表示出来,并按从小到大的顺序并用“<”号连接起来: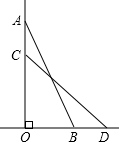 如图,一个25m长的梯子AB,斜靠在一竖直的墙AO上,这时的AO距离为24m,如果梯子的顶端A沿墙下滑4m,那么梯子底端B向外移多少m?
如图,一个25m长的梯子AB,斜靠在一竖直的墙AO上,这时的AO距离为24m,如果梯子的顶端A沿墙下滑4m,那么梯子底端B向外移多少m?