题目内容
4.若$\frac{1}{x+1999}-\frac{1}{x+1998}$=$\frac{1}{x+1997}-\frac{1}{x+1996}$,那么x=-1997$\frac{1}{2}$.分析 设x+1997=a,方程变形后,求出解得到a的值,确定出x的值,经检验即可得到分式方程的解.
解答 解:设x+1997=a,
方程变形得:$\frac{1}{a+2}$-$\frac{1}{a+1}$=$\frac{1}{a}$-$\frac{1}{a-1}$,即$\frac{1}{a+2}$-$\frac{1}{a}$=$\frac{1}{a+1}$-$\frac{1}{a-1}$,
整理得:$\frac{-2}{{a}^{2}+2a}$=$\frac{-2}{{a}^{2}-1}$,
可得a2+2a=a2-1,
解得:a=-$\frac{1}{2}$,即x+1997=-$\frac{1}{2}$,
则x=-1997$\frac{1}{2}$,
经检验x=-1997$\frac{1}{2}$是分式方程的解.
故答案为:-1997$\frac{1}{2}$.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 x,过点A(0,1)作y轴的垂线交直线
x,过点A(0,1)作y轴的垂线交直线 于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为( )
于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;…按此作法继续下去,则点A2015的坐标为( )
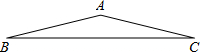 如图,△ABC中,AB=AC=2,∠B=15°,求等腰△ABC腰上高的值.
如图,△ABC中,AB=AC=2,∠B=15°,求等腰△ABC腰上高的值.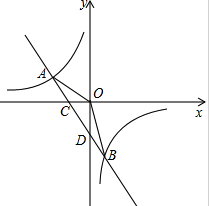 如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,与y轴交于点D,点A的坐标为(-2,1),点B的坐标为($\frac{1}{2}$,m).
如图,一次函数y=ax+b的图象与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,与x轴交于点C,与y轴交于点D,点A的坐标为(-2,1),点B的坐标为($\frac{1}{2}$,m).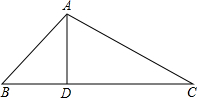 在Rt△ABC中,AB=12,BC=20,AD⊥BC,求cosB和AD的值.
在Rt△ABC中,AB=12,BC=20,AD⊥BC,求cosB和AD的值.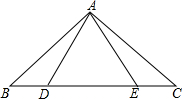 如图所示,已知△ABE≌△ACD,且AB=AC.
如图所示,已知△ABE≌△ACD,且AB=AC.