题目内容
12.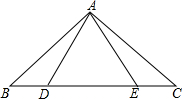 如图所示,已知△ABE≌△ACD,且AB=AC.
如图所示,已知△ABE≌△ACD,且AB=AC.(1)说明△ABE经过怎样的变换后可与△ACD重合;
(2)∠BAD与∠CAE有何关系?请说明理由;
(3)BD与CE相等吗?为什么?
分析 (1)由几何变换的类型说明即可,
(2)由三角形全等的性质求解即可,
(3)由三角形全等的性质求解即可.
解答 解:(1):(Ⅰ)沿BE边上的高向右翻折即可得到.
(Ⅱ)沿过E(B)点垂直BE所在的直线向右(左)翻折,再向右(左)平移即可得到△ACD
(2)∠BAD=∠CAE.
∵△ABE≌△ACD,
∴∠BAE=∠CAD,
∴∠BAE-∠DAE=∠CAD-∠DAE,
∴∠BAD=∠CAE,
(3)BD=CE,
∵△ABE≌△ACD,
∴BE=CD,
∴BE-DE=CD-DE,
∴BD=CE.
点评 本题主要考查了几何变换的类型及三角形全等的性质,解题的关键是熟记几何变换的类型及三角形全等的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.从正方形的四个顶点中,任取三个顶点连成三角形,对于事件M:“这个三角形是等腰三角形”.下列说法正确的是( )
| A. | 事件M为不可能事件 | B. | 事件M为必然事件 | ||
| C. | 事件M发生的概率为$\frac{1}{4}$ | D. | 事件M发生的概率为$\frac{1}{2}$ |
7.若函数y=ax2(a≠0)的图象与直线y=2x-3交于点(3,3b),则a,b的值分别是( )
| A. | 1,$\frac{1}{3}$ | B. | $\frac{1}{3}$,-1 | C. | -1,$\frac{1}{3}$ | D. | $\frac{1}{3}$,1 |
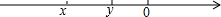 x,y表示的数在数轴上如图表示,试填入适当的不等号.
x,y表示的数在数轴上如图表示,试填入适当的不等号.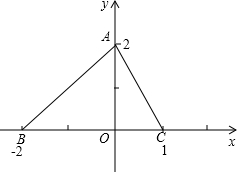 已知△ABC的顶点坐标分别为A(0,2),B(-2,0),C(1,0),O为坐标原点,试在AB和AC边上分别找一点D,E,使△DOE的周长最短,画出点D,E两点的位置图形,简述作图方法.
已知△ABC的顶点坐标分别为A(0,2),B(-2,0),C(1,0),O为坐标原点,试在AB和AC边上分别找一点D,E,使△DOE的周长最短,画出点D,E两点的位置图形,简述作图方法. 已知:AB=CD,AF=CE,DE⊥AC,BF⊥AC,BD与AC交于点G.求证:EG=FG.
已知:AB=CD,AF=CE,DE⊥AC,BF⊥AC,BD与AC交于点G.求证:EG=FG.