题目内容
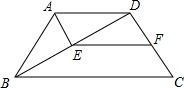 如图所示,在四边形ABCD中,AD∥BC.AB=DC=AD,∠ABC=∠C=60°,AE⊥BD于点E,F是CD的中点,求证:四边形AEFD是平行四边形.
如图所示,在四边形ABCD中,AD∥BC.AB=DC=AD,∠ABC=∠C=60°,AE⊥BD于点E,F是CD的中点,求证:四边形AEFD是平行四边形.考点:平行四边形的判定
专题:证明题
分析:根据等腰三角形的性质可得BE=DE,∠BAE=∠DAE=
∠BAD,再根据中位线的性质可得EF∥BC,再根据平行线的性质证明∠DAE=∠EFD,∠ADF=∠AEF,再根据两组对角分别相等的四边形是平行四边形可得结论.
| 1 |
| 2 |
解答:证明:∵AD=AB,AE⊥DB,
∴BE=DE,∠BAE=∠DAE=
∠BAD,
∵AD∥BC,∠ABC=60°,
∴∠BAD=120°,
∴∠DAE=60°,
∵F是CD的中点,
∴EF∥BC,
∴∠C=∠DFE=60°,
∵AD∥BC,
∴EF∥AD,
∴∠DAE+∠AEF=180°,∠ADF+∠EFD=180°,
∴∠AEF=∠ADF,
∴四边形AEFD是平行四边形.
∴BE=DE,∠BAE=∠DAE=
| 1 |
| 2 |
∵AD∥BC,∠ABC=60°,
∴∠BAD=120°,
∴∠DAE=60°,
∵F是CD的中点,
∴EF∥BC,
∴∠C=∠DFE=60°,
∵AD∥BC,
∴EF∥AD,
∴∠DAE+∠AEF=180°,∠ADF+∠EFD=180°,
∴∠AEF=∠ADF,
∴四边形AEFD是平行四边形.
点评:此题主要考查了平行四边形的判定,关键是掌握两组对角分别相等的四边形是平行四边形.

练习册系列答案
相关题目
已知AB、CD是⊙O的弦,且弦AB∥CD,若AB=8cm,CD=6cm,⊙O的半径为5cm,梯形ABCD的面积为( )
| A、49cm2 |
| B、1cm2 |
| C、49cm2或1cm2 |
| D、49cm2或7cm2 |
在数字:-32,5,0.32,1.6,0,-
中,负分数的个数是( )
| 1 |
| 2 |
| A、0个 | B、1个 | C、2个 | D、3个 |
 矩形AGFE∽矩形ABCD,AE、AD分别为它们的最短边,点F在AB上,且3AE=2AD.
矩形AGFE∽矩形ABCD,AE、AD分别为它们的最短边,点F在AB上,且3AE=2AD.