题目内容
 矩形AGFE∽矩形ABCD,AE、AD分别为它们的最短边,点F在AB上,且3AE=2AD.
矩形AGFE∽矩形ABCD,AE、AD分别为它们的最短边,点F在AB上,且3AE=2AD.(1)若矩形ABCD的面积为450cm2,求矩形AEFG的面积.
(2)求证:∠1=∠2.
考点:相似多边形的性质
专题:
分析:(1)首先利用相似多边形的对应边的关系得到相似比,从而利用面积的比等于相似比求得结论;
(2)利用相似多边形的性质得到AE:AD=AG:AB,从而得到△ADE∽△ABG,利用相似三角形的对应角相等求得结论.
(2)利用相似多边形的性质得到AE:AD=AG:AB,从而得到△ADE∽△ABG,利用相似三角形的对应角相等求得结论.
解答:解:(1)∵3AE=2AD,
∴
=
,
∵矩形AGFE∽矩形ABCD,
∴相似比为
=
,
∴面积的比为
,
∵矩形ABCD的面积为450cm2,
∴四边形AEFG的面积为200cm2;
(2)∵四边形ABCD为矩形,四边形AEFG∽四边形ADCB
∴∠DAB=∠EAG=90°,AE:AD=AG:AB,
∴∠DAE+∠EAF=∠GAB++∠EAF,
∴∠DAE=∠GAB,
∵AE:AD=AG:AB,
∴△ADE∽△ABG,
∴∠1=∠2.
∴
| AE |
| AD |
| 2 |
| 3 |
∵矩形AGFE∽矩形ABCD,
∴相似比为
| AE |
| AD |
| 2 |
| 3 |
∴面积的比为
| 4 |
| 9 |
∵矩形ABCD的面积为450cm2,
∴四边形AEFG的面积为200cm2;
(2)∵四边形ABCD为矩形,四边形AEFG∽四边形ADCB
∴∠DAB=∠EAG=90°,AE:AD=AG:AB,
∴∠DAE+∠EAF=∠GAB++∠EAF,
∴∠DAE=∠GAB,
∵AE:AD=AG:AB,
∴△ADE∽△ABG,
∴∠1=∠2.
点评:本题考查了相似多边形的性质,解题的关键是能够求得形似比,从而利用面积的比等于相似比求得结论.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
平方根等于本身的有( )
| A、0 | B、1 | C、0,±1 | D、0和1 |
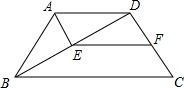 如图所示,在四边形ABCD中,AD∥BC.AB=DC=AD,∠ABC=∠C=60°,AE⊥BD于点E,F是CD的中点,求证:四边形AEFD是平行四边形.
如图所示,在四边形ABCD中,AD∥BC.AB=DC=AD,∠ABC=∠C=60°,AE⊥BD于点E,F是CD的中点,求证:四边形AEFD是平行四边形. 已知一水坝的横断面是梯形ABCD,下底BC长14m,斜坡AB的坡度为3:
已知一水坝的横断面是梯形ABCD,下底BC长14m,斜坡AB的坡度为3: