题目内容
已知AB、CD是⊙O的弦,且弦AB∥CD,若AB=8cm,CD=6cm,⊙O的半径为5cm,梯形ABCD的面积为( )
| A、49cm2 |
| B、1cm2 |
| C、49cm2或1cm2 |
| D、49cm2或7cm2 |
考点:垂径定理,勾股定理,梯形
专题:分类讨论
分析:梯形的高就是弦AB与CD之间的距离,根据垂径定理求得两弦的弦心距,当CD与AB在圆心的同侧时,梯形的高等于两弦心距的差,当CD与AB在圆心的两侧时,梯形的高等于两弦心距的和,根据梯形的面积公式即可求解.
解答: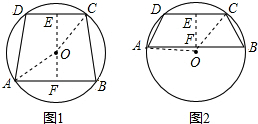 解:过点O作OE⊥CE于点E,交AB于点F,连接OA,OC,
解:过点O作OE⊥CE于点E,交AB于点F,连接OA,OC,
∵AB=8,CD=6,
∴CE=
BC=
×6=3,AF=
AB=
×8=4,
在Rt△COE中,OE=
=
=4;
在Rt△AOF中,OF=
=
=3,
当点AB,CD在圆心O的同侧时,如图1所示:
EF=OE+OF=4+3=7,S梯形ABCD=
(AB+CD)•EF=
×(6+8)×7=49;
当点AB,CD在圆心O的异侧时,如图2所示:
EF=OE+OF=4-3=1,S梯形ABCD=
(AB+CD)•EF=
×(6+8)×1=7;
∴梯形ABCD的面积为:7或49.
故选D.
 解:过点O作OE⊥CE于点E,交AB于点F,连接OA,OC,
解:过点O作OE⊥CE于点E,交AB于点F,连接OA,OC,∵AB=8,CD=6,
∴CE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△COE中,OE=
| OC2-CE2 |
| 52-32 |
在Rt△AOF中,OF=
| OA2-AF2 |
| 52-42 |
当点AB,CD在圆心O的同侧时,如图1所示:
EF=OE+OF=4+3=7,S梯形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
当点AB,CD在圆心O的异侧时,如图2所示:
EF=OE+OF=4-3=1,S梯形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
∴梯形ABCD的面积为:7或49.
故选D.
点评:本题考查的是垂径定理及勾股定理,在解答此题时要注意分类讨论,不要漏解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
用加减法解方程组
时,若要求消去y,则应( )
|
| A、①×3+②×2 |
| B、①×3-②×2 |
| C、①×5+②×3 |
| D、①×5-②×3 |
 如图是三个反比例函数y1=
如图是三个反比例函数y1=| k1 |
| x |
| k2 |
| x |
| k3 |
| x |
| A、k1>k2>k3 |
| B、k2>k1>k3 |
| C、k3>k2>k1 |
| D、k3>k1>k2 |
 如图,AB=AC,点D、E分别在AC、AB上,AF⊥CE,AG⊥BD,垂足分别为F、G,AF=AG,下列结论中:1、∠B=∠C;2、AD=AE;3、∠EAF=∠DAG;4、BE=CD.其中正确的结论是
如图,AB=AC,点D、E分别在AC、AB上,AF⊥CE,AG⊥BD,垂足分别为F、G,AF=AG,下列结论中:1、∠B=∠C;2、AD=AE;3、∠EAF=∠DAG;4、BE=CD.其中正确的结论是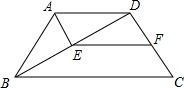 如图所示,在四边形ABCD中,AD∥BC.AB=DC=AD,∠ABC=∠C=60°,AE⊥BD于点E,F是CD的中点,求证:四边形AEFD是平行四边形.
如图所示,在四边形ABCD中,AD∥BC.AB=DC=AD,∠ABC=∠C=60°,AE⊥BD于点E,F是CD的中点,求证:四边形AEFD是平行四边形.