题目内容
3. 如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF
如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF(1)求证:△EBF≌△DFC;
(2)求证:四边形AEFD是平行四边形;
(3)①△ABC满足AB=AC时,四边形AEFD是菱形.(无需证明)
②△ABC满足∠BAC=150°时,四边形AEFD是矩形.(无需证明)
③△ABC满足AB=AC,∠BAC=150°时,四边形AEFD是正方形.(无需证明)
分析 (1)由△ABE与△BCF都为等边三角形,利用等边三角形的性质得到两对边相等,∠ABE=∠CBF=60°,利用等式的性质得到夹角相等,利用SAS得到△EBF与△DFC全等;
(2)利用(1)中全等三角形对应边相等得到EF=AC,再由三角形ADC为等边三角形得到三边相等,等量代换得到EF=AD,AE=DF,利用对边相等的四边形为平行四边形得到AEFD为平行四边形;
(3)①当AE=AD时,ADFE是菱形;
②当∠BAC=150°,由此可求得∠EAD的度数,则可得ADFE是矩形;
③当ADFE是正方形时,∠EAD=90°,且AE=AD,联立①②的结论即可.
解答  解:(1)∵△ABE、△BCF为等边三角形,
解:(1)∵△ABE、△BCF为等边三角形,
∴AB=BE=AE,BC=CF=FB,∠ABE=∠CBF=60°,
∴∠ABE-∠ABF=∠FBC-∠ABF,即∠CBA=∠FBE,
在△ABC和△EBF中,
$\left\{\begin{array}{l}{AB=EB}\\{∠CBA=∠FBE}\\{BC=BF}\end{array}\right.$,
∴△ABC≌△EBF(SAS),
∴EF=AC,
又∵△ADC为等边三角形,
∴CD=AD=AC,
∴EF=AD=DC,
同理可得△ABC≌△DFC,
∴DF=AB=AE=DF,
∴四边形AEFD是平行四边形;
∴∠FEA=∠ADF,
∴∠FEA+∠AEB=∠ADF+∠ADC,即∠FEB=∠CDF,
在△FEB和△CDF中,
$\left\{\begin{array}{l}{EF=DC}\\{∠FEB=∠CDF}\\{EB=FD}\end{array}\right.$.
∴△EBF≌△DFC(SAS),
(2)∵△EBF≌△DFC,
∴EB=DF,EF=DC.
∵△ACD和△ABE为等边三角形,
∴AD=DC,AE=BE,
∴AD=EF,AE=DF
∴四边形AEFD是平行四边形;
(3)①若AB=AC,则平行四边形AEFD是菱形;
此时AE=AB=AC=AD,即△ABC是等腰三角形;
故△ABC满足AB=AC时,四边形AEFD是菱形;
②若∠BAC=150°,则平行四边形AEFD是矩形;
由(1)知四边形AEFD是平行四边形,则∠EAD=90°时,可得平行四边形AEFD是矩形,
∴∠BAC=360°-60°-60°-90°=150°,
即△ABC满足∠BAC=150°时,四边形AEFD是矩形;
③综合①②的结论知:当△ABC是顶角∠BAC是150°的等腰三角形时,四边形AEFD是正方形.
故答案是:①AB=AC;
②∠BAC=150°;
③AB=AC,∠BAC=150°.
点评 考查了平行四边形及特殊平行四边形的判定,熟练掌握特殊四边形的判定方法和性质是解答此题的关键.

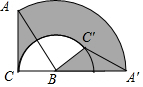 如图,将斜边长为4,∠A为30°角的Rt△ABC绕点B顺时针旋转120°得到△A′C′B,弧$\widehat{AA′}$、$\widehat{CC′}$是旋转过程中A、C的运动轨迹,则图中阴影部分的面积为( )
如图,将斜边长为4,∠A为30°角的Rt△ABC绕点B顺时针旋转120°得到△A′C′B,弧$\widehat{AA′}$、$\widehat{CC′}$是旋转过程中A、C的运动轨迹,则图中阴影部分的面积为( )| A. | 4π+2$\sqrt{3}$ | B. | $\frac{16}{3}$π-2$\sqrt{3}$ | C. | $\frac{16}{3}$π+2$\sqrt{3}$ | D. | 4π |
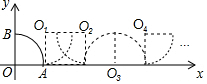 如图,点A(2,0),B(0,2),将扇形AOB沿x轴正方向做无滑动的滚动,在滚动过程中点O的对应点依次记为点O1,点O2,点O3…,则O10的坐标是( )
如图,点A(2,0),B(0,2),将扇形AOB沿x轴正方向做无滑动的滚动,在滚动过程中点O的对应点依次记为点O1,点O2,点O3…,则O10的坐标是( )| A. | (16+4π,0) | B. | (14+4π,2) | C. | (14+3π,2) | D. | (12+3π,0) |
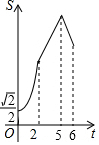
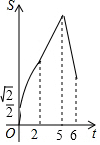
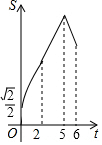
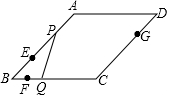 如图,在菱形ABCD中,∠ABC=45°,AB=6,点E、F、G分别是AB、BC、DC上的点,其中BE=DG=2,BF=1.点P从E点出发,以每秒2个单位长度沿折线EA-AD-DG运动;点Q以每秒1个单位沿折线FC-CG运动,当其中一个点到达后,另一个点也停止运动,设△BPQ的面积为S,点P,Q的运动时间为t秒,则S与t的函数关系的大致图象是( )
如图,在菱形ABCD中,∠ABC=45°,AB=6,点E、F、G分别是AB、BC、DC上的点,其中BE=DG=2,BF=1.点P从E点出发,以每秒2个单位长度沿折线EA-AD-DG运动;点Q以每秒1个单位沿折线FC-CG运动,当其中一个点到达后,另一个点也停止运动,设△BPQ的面积为S,点P,Q的运动时间为t秒,则S与t的函数关系的大致图象是( )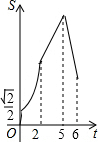
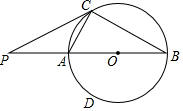 在圆O中,AC是圆的弦,AB是圆的直径,AB=6,∠ABC=30°,过点C作圆的切线交BA的延长线于点P,连接BC.
在圆O中,AC是圆的弦,AB是圆的直径,AB=6,∠ABC=30°,过点C作圆的切线交BA的延长线于点P,连接BC.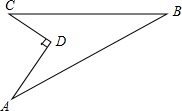 我校要对如图所示的一块地进行绿化,已知AD=4米,CD=3米,AD⊥DC,AB=13米,BC=12米,求这块地的面积.
我校要对如图所示的一块地进行绿化,已知AD=4米,CD=3米,AD⊥DC,AB=13米,BC=12米,求这块地的面积.