题目内容
11.已知关于x的方程x2+(3-m)x+$\frac{{m}^{2}}{4}$=0没有实数根,则m的取值范围是m>$\frac{3}{2}$.分析 根据判别式的意义得到(3-m)2-4•$\frac{{m}^{2}}{4}$<0,然后解关于m的一元一次不等式即可.
解答 解:根据题意得(3-m)2-4•$\frac{{m}^{2}}{4}$<0,
解得m>$\frac{3}{2}$.
故答案为m>$\frac{3}{2}$.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
相关题目
16. 如图是某个几何体的三视图,该几何体是( )
如图是某个几何体的三视图,该几何体是( )
 如图是某个几何体的三视图,该几何体是( )
如图是某个几何体的三视图,该几何体是( )| A. | 圆锥 | B. | 三棱锥 | C. | 四棱锥 | D. | 四棱柱 |
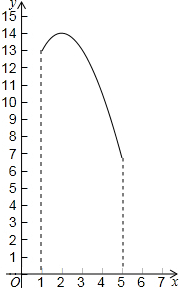
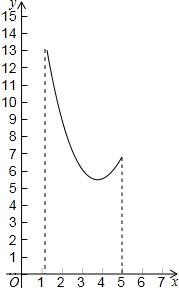
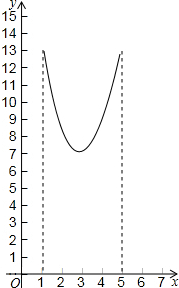
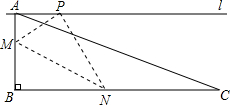 如图,在三角形纸片ABC中,∠ABC=90°,AB=5,BC=13,过点A,作直线l∥BC,折叠三角形纸片ABC,使点B落在直线l上的P处,折痕为MN.当点P在直线l上移动时,折痕的端点M、N也随之移动.若限定端点M、N分别在AB、BC边上移动,若设AP的长为x,MN的长为y,则下列选项,能表示y与x之间的函数关系的大致图象是( )
如图,在三角形纸片ABC中,∠ABC=90°,AB=5,BC=13,过点A,作直线l∥BC,折叠三角形纸片ABC,使点B落在直线l上的P处,折痕为MN.当点P在直线l上移动时,折痕的端点M、N也随之移动.若限定端点M、N分别在AB、BC边上移动,若设AP的长为x,MN的长为y,则下列选项,能表示y与x之间的函数关系的大致图象是( )
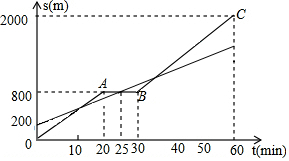 小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2000m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.
小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2000m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象. 如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF
如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF 如图,已知△ABC内接于⊙O,AB是直径,OD⊥BC于点D,延长DO交⊙O于F,连接OC,AF.
如图,已知△ABC内接于⊙O,AB是直径,OD⊥BC于点D,延长DO交⊙O于F,连接OC,AF.