题目内容
8.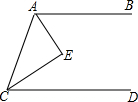 如图,AB∥CD,AE、CE分别是∠BAC和∠ACD的平分线,AE、CE相交于E,判断△ACE的形状,并说明理由.
如图,AB∥CD,AE、CE分别是∠BAC和∠ACD的平分线,AE、CE相交于E,判断△ACE的形状,并说明理由.
分析 先根据平行线的性质得出∠BAC+∠ACD=18°,再由角平分线的性质可得出∠EAC+∠ACE=90°,根据三角形内角和定理即可得出结论.
解答 解:△ACE是直角三角形.
理由:∵AB∥CD,
∴∠BAC+∠ACD=180°.
∵∠BAC的平分线和∠ACD的平分线交于点E,
∴∠EAC+∠ACE=$\frac{1}{2}$(∠BAC+∠ACD)=90°,
∴∠AEC=180°-90°=90°,
∴△AEC是直角三角形.
点评 本题考查的是平行线的性质以及角平分线的定义的运用,解题时注意:两直线平行,同旁内角互补.

练习册系列答案
相关题目
20.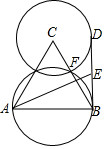 如图,已知等边△ABC的边长为4,以AB为直径的圆交BC于点F,以C为圆心,CF的长为半径作圆,D是⊙C上一动点,E为BD的中点,当AE最大时,BD的长为( )
如图,已知等边△ABC的边长为4,以AB为直径的圆交BC于点F,以C为圆心,CF的长为半径作圆,D是⊙C上一动点,E为BD的中点,当AE最大时,BD的长为( )
 如图,已知等边△ABC的边长为4,以AB为直径的圆交BC于点F,以C为圆心,CF的长为半径作圆,D是⊙C上一动点,E为BD的中点,当AE最大时,BD的长为( )
如图,已知等边△ABC的边长为4,以AB为直径的圆交BC于点F,以C为圆心,CF的长为半径作圆,D是⊙C上一动点,E为BD的中点,当AE最大时,BD的长为( )| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{5}$ | C. | 2$\sqrt{3}$+1 | D. | 6 |
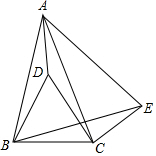 如图,在△ABC中,AB=AC,点D在△ABC内,BD=BC,∠DBC=60°,点E在△ABC外,∠BCE=150°,∠ABE=60°.
如图,在△ABC中,AB=AC,点D在△ABC内,BD=BC,∠DBC=60°,点E在△ABC外,∠BCE=150°,∠ABE=60°.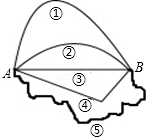 如图,从A地到B地共有五条路,人们常常选择第③条,请用几何知识解释原因两点之间,线段最短.
如图,从A地到B地共有五条路,人们常常选择第③条,请用几何知识解释原因两点之间,线段最短.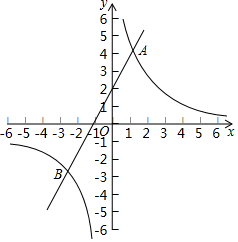 如图,直线y=2x+n与双曲线y=$\frac{m}{x}$(m≠0)交于A,B两点,且点A的坐标为(1,4).
如图,直线y=2x+n与双曲线y=$\frac{m}{x}$(m≠0)交于A,B两点,且点A的坐标为(1,4).