题目内容
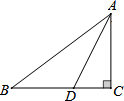
11. 如图所示,△ABC为等边三角形,AD∥BC,CD⊥AD,若△ABC的周长为36cm,则AD的长为6cm.
如图所示,△ABC为等边三角形,AD∥BC,CD⊥AD,若△ABC的周长为36cm,则AD的长为6cm.
分析 根据等边三角形的性质求出AC和∠ACB,根据平行线性质和垂直求出∠ACD=30°,∠D=90°,根据含30°角的直角三角形性质求出即可.
解答 解:∵△ABC为等边三角形,△ABC的周长为36cm,
∴AC=BC=AB=12cm,∠ACB=60°,
∵AD∥BC,CD⊥AD,
∴∠D=∠DCB=90°,
∴∠ACD=90°-60°=30°,
∴AD=$\frac{1}{2}$AC=6cm.
故答案为:6cm.
点评 本题考查了等边三角形的性质,平行线性质,垂直定义,含30°角的直角三角形性质的应用,能求出AD=$\frac{1}{2}$AC是解此题的关键.

练习册系列答案
相关题目
10.下列命题中,正确的个数是( )
①直径是弦,弦是直径;
②弦是圆上的两点间的部分;
③半圆是弧,但弧不一定是半圆;
④直径相等的两个圆是等圆;
⑤等于半径两倍的线段是直径.
①直径是弦,弦是直径;
②弦是圆上的两点间的部分;
③半圆是弧,但弧不一定是半圆;
④直径相等的两个圆是等圆;
⑤等于半径两倍的线段是直径.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
6. 如图,在Rt△ABC中,AD平分∠BAC,AC=BC,∠C=Rt∠,那么$\frac{AC}{DC}$的值为( )
如图,在Rt△ABC中,AD平分∠BAC,AC=BC,∠C=Rt∠,那么$\frac{AC}{DC}$的值为( )
 如图,在Rt△ABC中,AD平分∠BAC,AC=BC,∠C=Rt∠,那么$\frac{AC}{DC}$的值为( )
如图,在Rt△ABC中,AD平分∠BAC,AC=BC,∠C=Rt∠,那么$\frac{AC}{DC}$的值为( )| A. | ($\sqrt{2}$-1):1 | B. | ($\sqrt{2}$+1):1 | C. | $\sqrt{2}$:1 | D. | 2:1 |
20.下列各式中,没有意义的是( )
| A. | $-\sqrt{3}$ | B. | $\sqrt{-3}$ | C. | $\sqrt{{{(-3)}^2}}$ | D. | $\root{3}{-1}$ |
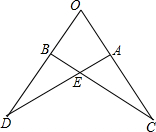 如图,若△OBC≌△OAD,且AC=6,OD=10,则OA=4.
如图,若△OBC≌△OAD,且AC=6,OD=10,则OA=4.
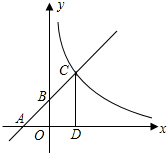 如图所示,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A,B两点,且与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限交于C点,CD垂直于x轴,垂足为D,若OA=OB=OD=3,
如图所示,已知一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于A,B两点,且与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限交于C点,CD垂直于x轴,垂足为D,若OA=OB=OD=3,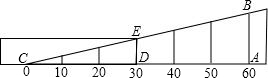 如图,测量小玻璃管口径的量具ABC中,AB的长是10毫米,AC被分成6等份,如果小管口DE正好对着量具上3份处(DE∥AB),那么小管口径DE的长是5毫米.
如图,测量小玻璃管口径的量具ABC中,AB的长是10毫米,AC被分成6等份,如果小管口DE正好对着量具上3份处(DE∥AB),那么小管口径DE的长是5毫米.