题目内容
7.关于x的一元二次方程x2-6x+5(m-5)=0的两个实数根为x1,x2,且2x1+x2=7,则m的值为6.分析 根据根与系数的关系可以求得x1和x2的值,从而可以求得m的值.
解答 解:∵方程x2-6x+5(m-5)=0的两个实数根为x1,x2,
∴x1+x2=-$\frac{-6}{1}$=6,x1•x2=5(m-5),
∵2x1+x2=7,
∴x1=1,x2=5,
∴1×5=5(m-5),
解得,m=6,
故答案为:6.
点评 本题考查根与系数的关系,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
18.已知多项式ax5+bx3+cx-9,当x=3时的值为16,那么当x=-3时,求此多项式的值为( )
| A. | -34 | B. | -16 | C. | 16 | D. | 34 |
15.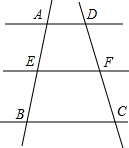 如图,AD∥EF∥BC,下列选项不成立的是( )
如图,AD∥EF∥BC,下列选项不成立的是( )
 如图,AD∥EF∥BC,下列选项不成立的是( )
如图,AD∥EF∥BC,下列选项不成立的是( )| A. | $\frac{AE}{EB}$=$\frac{DF}{FC}$ | B. | $\frac{BE}{CF}$=$\frac{AE}{DF}$ | C. | $\frac{AE}{AB}$=$\frac{AD}{BC}$ | D. | $\frac{AE}{DF}$=$\frac{AB}{DC}$ |
4.若实数x,y,z满足关系式2x+3y-z=0,5x-2y-2z=0,则x:y:z的值为( )
| A. | 2:3:1 | B. | 5:2:2 | C. | 8:1:19 | D. | 8:1:1 |

 二次函数y=ax2(a≠0)的图象如图所示,则不等式ax+a>0的解集是x>-1.
二次函数y=ax2(a≠0)的图象如图所示,则不等式ax+a>0的解集是x>-1.