题目内容
13．若关于x的方程$\frac{1}{x-2}$+$\frac{k}{x+2}$=$\frac{3}{{x}^{2}-4}$有增根，求增根和k的值．分析 增根是分式方程化为整式方程后产生的使分式方程的分母为0的根．有增根，那么最简公分母（x-2）（x+2）=0，所以增根是x=2或-2，把增根代入化为整式方程的方程即可求出k的值．
解答 解：方程两边都乘（x-2）（x+2），得
x+2+k（x-2）=3，
∵原方程有增根，
∴最简公分母（x-2）（x+2）=0，
∴x=2或-2，
把x=2代入整式方程得：4=3，故矛盾，
∴x≠2，
把x=-2代入整式方程得：k=-$\frac{3}{4}$．
∴x=-2，k=-$\frac{3}{4}$．
点评 本题考查了分式方程的增根，增根问题可按如下步骤进行：
①根据最简公分母确定增根；
②化分式方程为整式方程；
③把增根代入整式方程即可求得相关字母的值．
练习册系列答案
相关题目
3．李老师做了个长方形教具，其中一边长为2a+b，另一边长为a-b，则该长方形的面积为（ ）
| A． | 6a+b | B． | 2a2-ab-b2 | C． | 3a | D． | 10a-b |
如图，矩形ABCD两条对角线相交于点O，∠AOD=120°，AB=2，则矩形的对角线AC的长是4．
如图，若AB∥CD，CE平分∠DCB，且∠B+∠DAB=180°．证明：∠E=∠3．
8．解分式方程$\frac{2}{x+1}+\frac{3}{x-1}=\frac{6}{{{x^2}-1}}$，分以下四步，其中，错误的一步是（ ）
| A． | 方程两边分式的最简公分母是（x-1）（x+1） | |
| B． | 方程两边都乘以（x-1）（x+1），得整式方程2（x-1）+3（x+1）=6 | |
| C． | 解这个整式方程，得x=1 | |
| D． | 原方程的解为x=1 |
18．下列二次根式，能与$\sqrt{3}$合并的是（ ）
| A． | $\sqrt{18}$ | B． | $\sqrt{20}$ | C． | $\sqrt{48}$ | D． | $\sqrt{\frac{1}{2}}$ |
5．
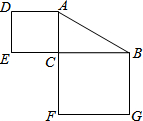如图，在Rt△ABC中，∠C=90°，若AB=15，则正方形ADEC和正方形BCFG的面积和为（ ）
如图，在Rt△ABC中，∠C=90°，若AB=15，则正方形ADEC和正方形BCFG的面积和为（ ）| A． | 225 | B． | 200 | C． | 250 | D． | 150 |
3．下列二次根式中是最简二次根式的是（ ）
| A． | $\sqrt{4x}$ | B． | $\sqrt{\frac{1}{x}}$ | C． | $\sqrt{{x}^{2}+{y}^{2}-2xy}$ | D． | $\sqrt{{x}^{2}-{y}^{2}}$ |