题目内容
9. 如图,PA、PB切⊙O于两点,若∠APB=60°,⊙O的半径为4,则阴影部分的面积为16$\sqrt{3}$-$\frac{16π}{3}$.
如图,PA、PB切⊙O于两点,若∠APB=60°,⊙O的半径为4,则阴影部分的面积为16$\sqrt{3}$-$\frac{16π}{3}$.
分析 连接OA,OB,OP,由题意可知阴影部分的面积等于四边形OAPB的面积减去扇形AOB的面积,问题得解.
解答 解:连接OA,OB,OP.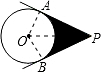
根据切线长定理得∠APO=30°,
∴OP=2OA=8,AP=OP•cos30°=4$\sqrt{3}$,∠AOP=60°.
∴四边形的面积=2S△AOP=2×$\frac{1}{2}$×4×4$\sqrt{3}$=16$\sqrt{3}$;扇形的面积是=$\frac{120×π×16}{360}$=$\frac{16π}{3}$,
∴阴影部分的面积=16$\sqrt{3}$-$\frac{16π}{3}$.
点评 此题综合运用了切线长定理、切线的性质定理以及30°的直角三角形的性质.关键是熟练运用扇形的面积计算公式,能够把四边形的面积转化为三角形的面积计算.

练习册系列答案
相关题目
17.|$\sqrt{3}$-1|-$\sqrt{(1-\sqrt{3})^{2}}$的值是( )
| A. | 0 | B. | -2 | C. | -2$\sqrt{3}$ | D. | 以上都不对 |
20.下列根式是最简二次根式的是( )
| A. | $\sqrt{a^2}$ | B. | $\sqrt{a+2}$ | C. | $\sqrt{\frac{1}{a}}$ | D. | $\sqrt{{a^2}b}$ |
14.下列各点在函数y=-$\frac{6}{x}$图象上的是( )
| A. | (-2,-3) | B. | (3,2) | C. | (-1,6) | D. | (-6,-1) |
 如图是一个台阶的示意图,台阶横长5m,如果要在台阶上铺地毯,那么至少要买地毯多少平方米?
如图是一个台阶的示意图,台阶横长5m,如果要在台阶上铺地毯,那么至少要买地毯多少平方米? 如图,直线y=kx+b经过点A(-1,-2)和点B(-2,0),直线y=2x过点A,不等式2x<kx+b<0的解集为-2<x<-1.
如图,直线y=kx+b经过点A(-1,-2)和点B(-2,0),直线y=2x过点A,不等式2x<kx+b<0的解集为-2<x<-1. 如图,在⊙O内接四边形ABCD中,∠ABC=60°,AB=BC=6,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为11$\sqrt{3}$,则△BEF的面积为5$\sqrt{3}$.
如图,在⊙O内接四边形ABCD中,∠ABC=60°,AB=BC=6,E、F分别是AD、CD的中点,连接BE、BF、EF.若四边形ABCD的面积为11$\sqrt{3}$,则△BEF的面积为5$\sqrt{3}$.