题目内容
为了改善住房条件,小亮的父母考察了某小区的A、B两套楼房,A套楼房在第3层楼,B套楼房在第5层楼,B套楼房的面积比A套楼房的面积大24平方米,两套楼房的房价相同,第3层楼和第5层楼的房价分别是平均价的1.1倍和0.9倍,求两户型楼房的面积.
考点:一元一次方程的应用
专题:
分析:设A套楼房的面积为xm2,则B套楼房面积为(x+24)m2,平均房价为1,等量关系为:1.1×1×A套楼房的面积=0.9×1×B套楼房的面积,根据等量关系可列方程,解方程即可.
解答:解:设A套楼房的面积为xm2,则B套楼房面积为(x+24)m2.
依题意列方程:
1.1×1x=0.9×1(x+24),
解得x=108.
B套面积为:108+24=132(m2).
答:A套楼房的面积为108m2,则B套楼房面积为132m2.
依题意列方程:
1.1×1x=0.9×1(x+24),
解得x=108.
B套面积为:108+24=132(m2).
答:A套楼房的面积为108m2,则B套楼房面积为132m2.
点评:本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
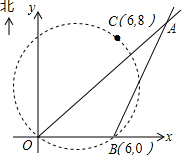 在某张航海图上,标明了三个观测点的坐标,如图,O(0,0)、B(6,0)、C(6,8),由三个观测点确定的圆形区域是海洋生物保护区.
在某张航海图上,标明了三个观测点的坐标,如图,O(0,0)、B(6,0)、C(6,8),由三个观测点确定的圆形区域是海洋生物保护区.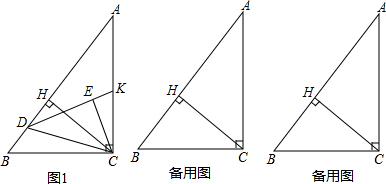
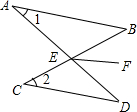 如图,AB∥CD,AD与BC交于点E,EF是∠BED的平分线,若∠1=29°,∠2=47°,则∠BEF=
如图,AB∥CD,AD与BC交于点E,EF是∠BED的平分线,若∠1=29°,∠2=47°,则∠BEF=