题目内容
13. 如图,△ABC中,∠A=90°,AB=AC,D为AC中点,F为BC上一点,∠ADB=∠FDC,试判断AF与BD的位置关系,并说明理由.
如图,△ABC中,∠A=90°,AB=AC,D为AC中点,F为BC上一点,∠ADB=∠FDC,试判断AF与BD的位置关系,并说明理由.
分析 作AG平分∠BAC,交BD于点M,首先证明△AMD≌△CFD,进而得出△BAM≌△CAF,从而证明AF⊥BD.
解答 证明:如图,作AG平分∠BAC,交BD于点M,
∵∠A=90°,AB=AC,
∴∠DAM=∠3=∠DCF=45°,
∵D为AC中点,
∴DC=DA,
在△AMD和△CFD中,
$\left\{\begin{array}{l}{∠DAM=∠DCF}\\{DC=DA}\\{∠ADB=∠FDC}\end{array}\right.$,
∴△AMD≌△CFD(ASA),
∴AM=CF,
在△BAM和△CAF中,
$\left\{\begin{array}{l}{AM=CF}\\{∠C=∠3}\\{AC=BA}\end{array}\right.$,
∴△BAM≌△CAF(SAS),
∴∠1=∠2,
∵∠2+∠4=90°,
∴∠1+∠4=90°,
∴∠AED=90°,
即AF⊥BD.
点评 本题考查了等腰直角三角形的性质,以及全等三角形的判定与性质.对条件充分认识和对知识点的系统利用,添加合适的辅助线,构造全等三角形是解本题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
4.如果把分式$\frac{{a}^{2}}{a-b}$中的a和b都扩大到原来的2倍,那么分式的值( )
| A. | 扩大到原来的2倍 | B. | 不变 | C. | 缩小为原来的$\frac{1}{2}$ | D. | 扩大到原来的4倍 |
1.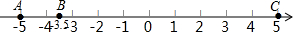 如图,在数轴上有三个点A、B、C,分别表示数-5,-3.5,5,现在点C不动,点A以每秒2个单位长度向点C运动,同时点B以每秒1.5个单位长度向点C运动,则先到达点C的点为( )
如图,在数轴上有三个点A、B、C,分别表示数-5,-3.5,5,现在点C不动,点A以每秒2个单位长度向点C运动,同时点B以每秒1.5个单位长度向点C运动,则先到达点C的点为( )
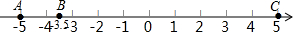 如图,在数轴上有三个点A、B、C,分别表示数-5,-3.5,5,现在点C不动,点A以每秒2个单位长度向点C运动,同时点B以每秒1.5个单位长度向点C运动,则先到达点C的点为( )
如图,在数轴上有三个点A、B、C,分别表示数-5,-3.5,5,现在点C不动,点A以每秒2个单位长度向点C运动,同时点B以每秒1.5个单位长度向点C运动,则先到达点C的点为( )| A. | 点A | B. | 点B | C. | 同时到达 | D. | 无法确定 |
5.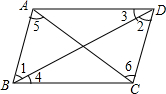 如图,若∠3=∠4,则下列结论:①AB∥CD;②AD∥BC;③∠1=∠2;④∠5=∠6,其中正确的有( )
如图,若∠3=∠4,则下列结论:①AB∥CD;②AD∥BC;③∠1=∠2;④∠5=∠6,其中正确的有( )
 如图,若∠3=∠4,则下列结论:①AB∥CD;②AD∥BC;③∠1=∠2;④∠5=∠6,其中正确的有( )
如图,若∠3=∠4,则下列结论:①AB∥CD;②AD∥BC;③∠1=∠2;④∠5=∠6,其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
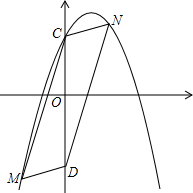 如图,已知抛物线y=-x2+2x+3与坐标轴交于A,B,C三点,点D,C关于原点对称,点M,N是抛物线上两点,且四边形CMDN为平行四边形,求点M,N的坐标.
如图,已知抛物线y=-x2+2x+3与坐标轴交于A,B,C三点,点D,C关于原点对称,点M,N是抛物线上两点,且四边形CMDN为平行四边形,求点M,N的坐标.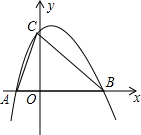 如图,二次函数y=-x2+ax+b的图象与x轴交于A(-$\frac{1}{2}$,O),B(2,0)两点,且与y轴交于点C.
如图,二次函数y=-x2+ax+b的图象与x轴交于A(-$\frac{1}{2}$,O),B(2,0)两点,且与y轴交于点C.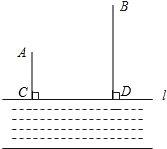 如图,A,B两个小镇在河流CD的同侧,到河的距离分别为AC=6千米,BD=14千米,且CD=15千米,现要在河边建一自来水厂,同时向A,B两镇供水,铺设水管的费用为每千米3万元,请你在河流CD上选择水厂的位置M,使铺设水管的费用最省,并求出总费用是多少?
如图,A,B两个小镇在河流CD的同侧,到河的距离分别为AC=6千米,BD=14千米,且CD=15千米,现要在河边建一自来水厂,同时向A,B两镇供水,铺设水管的费用为每千米3万元,请你在河流CD上选择水厂的位置M,使铺设水管的费用最省,并求出总费用是多少?