题目内容
2.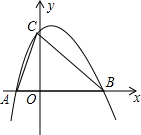 如图,二次函数y=-x2+ax+b的图象与x轴交于A(-$\frac{1}{2}$,O),B(2,0)两点,且与y轴交于点C.
如图,二次函数y=-x2+ax+b的图象与x轴交于A(-$\frac{1}{2}$,O),B(2,0)两点,且与y轴交于点C.(1)求该抛物线的解析式;
(2)判断△ABC的形状.
分析 (1)将A、B的坐标代入抛物线的解析式中即可确定抛物线的解析式;
(2)由抛物线的解析式得到C点坐标,进而可求出AC、BC、AB的长,然后再判断△ABC的形状.
解答 解:(1)由题意得:
$\left\{\begin{array}{l}{-\frac{1}{4}-\frac{1}{2}a+b=0}\\{-4+2a+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=\frac{3}{2}}\\{b=1}\end{array}\right.$,
∴抛物线的解析式为y=-x2+$\frac{3}{2}$x+1;
(2)∵y=-x2+$\frac{3}{2}$x+1,
∴C(0,1);
∴AC2=$\frac{1}{4}$+1=$\frac{5}{4}$,BC2=1+4=5,AB2=(2+$\frac{1}{2}$)2=$\frac{25}{4}$;
∵AC2+BC2=AB2,
∴△ABC是直角三角形.
点评 本题主要考查了待定系数法求函数表达式和勾股定理逆定理,求出函数表达式是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.小婷从标有1到9序号的9张卡片中任意抽取一张,抽到序号是3的倍数的概率是( )
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{3}$ | D. | 1 |
 如图,OA⊥OB,若射线OA的方向为北偏东65°,则射线OB的方向为南偏东25°.
如图,OA⊥OB,若射线OA的方向为北偏东65°,则射线OB的方向为南偏东25°. 如图,△ABC中,∠A=90°,AB=AC,D为AC中点,F为BC上一点,∠ADB=∠FDC,试判断AF与BD的位置关系,并说明理由.
如图,△ABC中,∠A=90°,AB=AC,D为AC中点,F为BC上一点,∠ADB=∠FDC,试判断AF与BD的位置关系,并说明理由.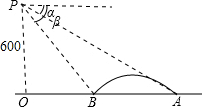 如图,直升飞机在大桥AB的上方P点处,此时飞机离地面高度PO=600米,且A、B、O三点在一条直线上,测得大桥两端A、B的俯角分别为α=30°,β=45°,求大桥的长AB.
如图,直升飞机在大桥AB的上方P点处,此时飞机离地面高度PO=600米,且A、B、O三点在一条直线上,测得大桥两端A、B的俯角分别为α=30°,β=45°,求大桥的长AB. 如图,∠1=45°,∠2=135°,直线AB与CD平行吗?试着说出你的理由.
如图,∠1=45°,∠2=135°,直线AB与CD平行吗?试着说出你的理由. 如图,四边形PMNQ是正方形,△ABC的高AD=6cm,BC=12cm,则正方形PMNQ的边长是4cm.
如图,四边形PMNQ是正方形,△ABC的高AD=6cm,BC=12cm,则正方形PMNQ的边长是4cm.